Calcular el area de la region acotada por la curva
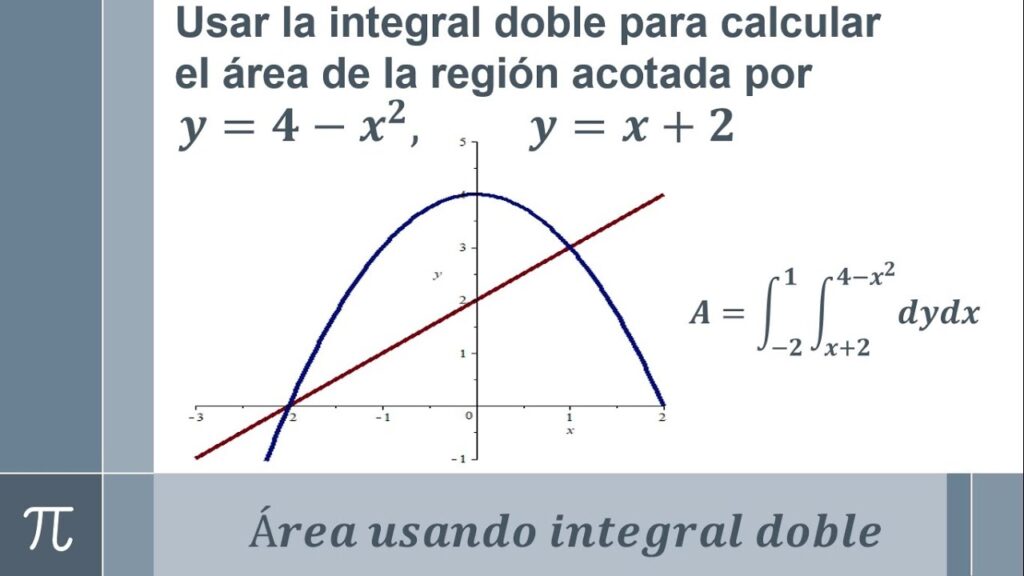
Cuando se trabaja con cálculo integral, una de las tareas más comunes es calcular el área de una región acotada por una curva en un plano cartesiano. Este proceso puede ser un poco confuso al principio, pero con un poco de práctica y comprensión del concepto, se vuelve más fácil de entender.
En este artículo, vamos a repasar los pasos necesarios para calcular el área de una región acotada por una curva. También vamos a comparar el proceso con una tabla HTML para facilitar la comprensión.
- Paso 1: Identificar la curva
- Paso 2: Establecer los límites de integración
- Paso 3: Crear la integral
- Paso 4: Resolver la integral
- Paso 5: Interpretar el resultado
- Preguntas frecuentes
- ¿Cómo sé si una curva está bien definida en un intervalo?
- ¿Por qué es importante establecer los límites de integración?
- ¿Cómo se crea la integral para calcular el área de una región acotada por una curva?
- ¿Qué técnicas de integración se pueden utilizar para resolver la integral?
- ¿Cómo se verifica que el resultado de la integral tenga sentido en el contexto del problema?
Paso 1: Identificar la curva
El primer paso para calcular el área de una región acotada por una curva es identificar la curva en cuestión. La curva puede ser una función, una ecuación, una serie de puntos, etc. Una vez que se ha identificado la curva, es importante asegurarse de que esté bien definida en el intervalo en cuestión.
Paso 2: Establecer los límites de integración
El siguiente paso es establecer los límites de integración. Estos límites determinan el intervalo en el que se va a integrar la función. Los límites de integración pueden ser dados o pueden tener que ser determinados a partir de la curva.
Paso 3: Crear la integral
Una vez que se han establecido los límites de integración, es posible crear la integral. La integral representa el área de la región acotada por la curva. La integral debe ser creada utilizando la función que representa la curva, los límites de integración y el diferencial de área.
Paso 4: Resolver la integral
El siguiente paso es resolver la integral utilizando técnicas de integración. Esto puede ser un proceso largo y complicado, así que es importante ser preciso y cuidadoso al realizar este paso.
Paso 5: Interpretar el resultado
Una vez que se ha resuelto la integral, es posible interpretar el resultado. El resultado de la integral representa el área de la región acotada por la curva. Es importante verificar que el resultado tenga sentido en el contexto del problema.
A continuación, vamos a comparar el proceso de calcular el área de una región acotada por una curva con una tabla HTML. La tabla muestra los pasos necesarios para calcular el área de la región acotada por la función y=x^2 en el intervalo [0,1].
| Paso | Descripción | Tabla HTML |
|---|---|---|
| 1 | Identificar la curva | y=x^2 |
| 2 | Establecer los límites de integración | [0,1] |
| 3 | Crear la integral | ∫01 x^2 dx |
| 4 | Resolver la integral | ∫01 x^2 dx = 1/3 |
| 5 | Interpretar el resultado | El área de la región acotada por y=x^2 en [0,1] es 1/3 unidades cuadradas. |
Como se puede ver en la tabla, el proceso de calcular el área de una región acotada por una curva puede ser fácilmente representado en una tabla HTML.
Preguntas frecuentes
¿Cómo sé si una curva está bien definida en un intervalo?
Una curva está bien definida en un intervalo si cumple con ciertas condiciones, como ser continua y diferenciable en el intervalo. Es importante revisar las propiedades de la curva antes de calcular su área.
¿Por qué es importante establecer los límites de integración?
Los límites de integración determinan el intervalo en el que se va a integrar la función. Si los límites de integración no están bien establecidos, es posible que se calcule el área de una región diferente a la deseada.
¿Cómo se crea la integral para calcular el área de una región acotada por una curva?
La integral se crea utilizando la función que representa la curva, los límites de integración y el diferencial de área. El diferencial de área depende de la geometría de la región y puede ser un rectángulo, un triángulo, etc.
¿Qué técnicas de integración se pueden utilizar para resolver la integral?
Existen diferentes técnicas de integración, como integración por partes, sustitución trigonométrica, fracciones parciales, entre otras. La técnica a utilizar depende de la complejidad de la función y de la habilidad del calculista.
¿Cómo se verifica que el resultado de la integral tenga sentido en el contexto del problema?
Es importante verificar que el resultado tenga sentido en el contexto del problema. Por ejemplo, si se está calculando el área de una región acotada por una curva, el resultado debe ser positivo y tener unidades cuadradas. También se debe verificar que el resultado tenga sentido geométrico.

Deja una respuesta