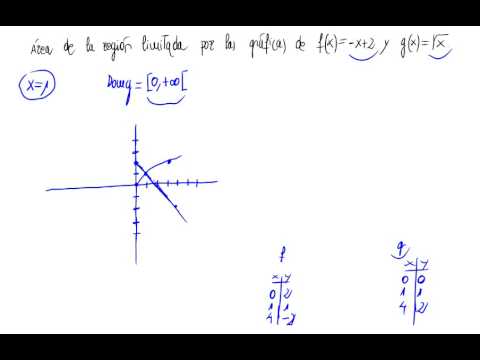
Calcular el area limitada por las graficas de las funciones

El cálculo del área limitada por las gráficas de las funciones es una de las tareas más comunes en el cálculo integral. En términos simples, esta tarea implica encontrar el área debajo de una curva en un intervalo específico. Esto puede ser útil en una variedad de situaciones, desde calcular la cantidad de pintura necesaria para cubrir una pared hasta entender la distribución de la población en una ciudad.

Para calcular el área limitada por las gráficas de las funciones, es necesario utilizar la integración. La integración es un proceso matemático que permite encontrar la función primitiva de una función dada. En términos simples, la función primitiva de una función es su antiderivada. Al encontrar la función primitiva de una función dada, es posible calcular el área limitada por su gráfica en un intervalo específico.

Para calcular el área limitada por las gráficas de las funciones, sigue estos pasos:

1. Identifica la función que deseas integrar y el intervalo en el que deseas calcular el área.
2. Encuentra la función primitiva de la función dada utilizando la integración.
3. Evalúa la función primitiva en los límites del intervalo dado.
4. Resta el valor de la función primitiva evaluada en el límite inferior del intervalo del valor de la función primitiva evaluada en el límite superior del intervalo.

Por ejemplo, supongamos que deseamos calcular el área limitada por la gráfica de la función y = x^2 en el intervalo [0, 2]. Primero, encontramos la función primitiva de la función dada utilizando la integración. La función primitiva de y = x^2 es (1/3)x^3. Luego, evaluamos la función primitiva en los límites del intervalo dado: (1/3)(2)^3 - (1/3)(0)^3. Finalmente, restamos el valor de la función primitiva evaluada en el límite inferior del intervalo del valor de la función primitiva evaluada en el límite superior del intervalo: (1/3)(2)^3 - (1/3)(0)^3 = (8/3) unidades cuadradas.

Es importante destacar que el cálculo del área limitada por las gráficas de las funciones puede ser complicado en algunos casos. Por ejemplo, si la función dada tiene una forma compleja o la región a calcular es irregular, puede ser necesario dividir la región en varias secciones y calcular el área de cada sección por separado. También es importante tener en cuenta que en algunos casos puede ser imposible encontrar una función primitiva para la función dada, lo que hace que el cálculo del área sea mucho más difícil.

En resumen, El cálculo del área limitada por las gráficas de las funciones es una tarea importante en el cálculo integral y puede ser útil en una variedad de situaciones en la vida cotidiana. Para calcular el área, es necesario utilizar la integración y seguir los pasos mencionados anteriormente. Sin embargo, es importante tener en cuenta que el cálculo del área puede ser complicado en algunos casos y puede requerir la división de la región en varias secciones o la utilización de técnicas avanzadas de integración.

Preguntas frecuentes

1. ¿Por qué es importante calcular el área limitada por las gráficas de las funciones?
Calcular el área limitada por las gráficas de las funciones puede ser útil en una variedad de situaciones en la vida cotidiana, desde calcular la cantidad de pintura necesaria para cubrir una pared hasta entender la distribución de la población en una ciudad.

2. ¿Qué es la integración?
La integración es un proceso matemático que permite encontrar la función primitiva de una función dada.

3. ¿Cómo se encuentra la función primitiva de una función?
La función primitiva de una función se encuentra utilizando la integración.

4. ¿Qué pasa si no se puede encontrar una función primitiva para la función dada?
Si no se puede encontrar una función primitiva para la función dada, el cálculo del área limitada por su gráfica puede ser mucho más difícil.

5. ¿Qué se debe hacer si la región a calcular es irregular?
Si la región a calcular es irregular, puede ser necesario dividir la región en varias secciones y calcular el área de cada sección por separado.