Como calcular el area de un triangulo con 3 puntos

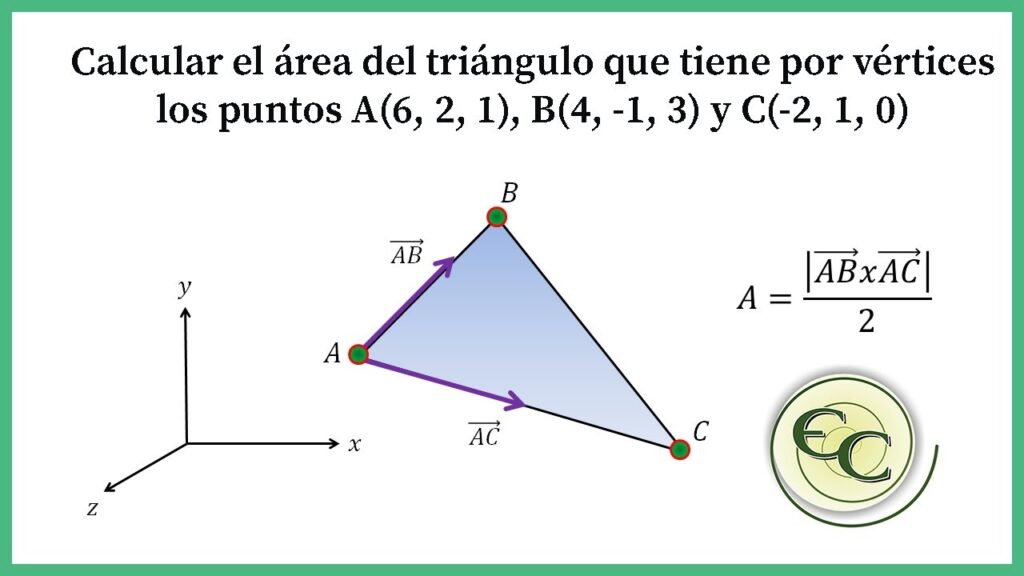
Si te encuentras en la necesidad de calcular el área de un triángulo con tres puntos, ¡no te preocupes! Es un cálculo muy sencillo que puedes realizar con facilidad. En este artículo te explicaremos paso a paso cómo hacerlo.

¿Qué necesitas para calcular el área de un triángulo con tres puntos?

Antes de comenzar, asegúrate de tener los siguientes elementos:

• Los tres puntos del triángulo: (x1, y1), (x2, y2) y (x3, y3).
• Una calculadora para realizar las operaciones matemáticas necesarias.

Paso 1: Identifica los tres puntos del triángulo

Lo primero que debes hacer es identificar los tres puntos que conforman el triángulo. Cada punto se representa por un par ordenado (x, y), donde "x" es la coordenada horizontal y "y" es la coordenada vertical.

Paso 2: Calcula la base del triángulo

Para calcular la base del triángulo, debes restar las coordenadas "x" del primer punto (x1) de las coordenadas "x" del segundo punto (x2).

Por ejemplo, si los puntos A y B tienen las coordenadas (2, 3) y (5, 3) respectivamente, la base del triángulo será:

base = x2 - x1
base = 5 - 2
base = 3

Paso 3: Calcula la altura del triángulo

La altura del triángulo es la distancia perpendicular entre la base y el tercer punto (x3, y3). Para calcularla, debes restar las coordenadas "y" de los dos primeros puntos.

Por ejemplo, si los puntos A y B tienen las coordenadas (2, 3) y (5, 3) respectivamente, y el punto C tiene las coordenadas (4, 5), la altura del triángulo será:

altura = y3 - y1
altura = 5 - 3
altura = 2

Paso 4: Calcula el área del triángulo

Una vez que tienes la base y la altura del triángulo, puedes calcular el área. La fórmula para calcular el área de un triángulo es:

área = (base * altura) / 2

Por lo tanto, si la base del triángulo es 3 y la altura es 2, el área del triángulo será:

área = (3 * 2) / 2
área = 3

Conclusión

Calcular el área de un triángulo con tres puntos puede parecer complicado al principio, pero siguiendo estos pasos es muy sencillo. Solo necesitas identificar los tres puntos, calcular la base y la altura y aplicar la fórmula del área.

Recuerda que para realizar este cálculo necesitas tener conocimientos básicos de geometría y matemáticas. Si tienes dudas, no dudes en consultar con un profesor o tutor.

Preguntas frecuentes

1. ¿Es posible calcular el área de un triángulo si solo se conocen dos puntos?

No, es necesario conocer los tres puntos del triángulo para poder calcular su área.

2. ¿Puedo usar una fórmula diferente para calcular el área de un triángulo?

Sí, existen otras fórmulas para calcular el área de un triángulo, como la fórmula de Herón. Sin embargo, la fórmula que explicamos en este artículo es la más sencilla y fácil de aplicar cuando se conocen los tres puntos del triángulo.

3. ¿Qué unidad de medida debo usar para las coordenadas de los puntos?

Depende de la situación. Si estás trabajando en un plano cartesiano, las coordenadas suelen ser números enteros. Si estás trabajando con coordenadas geográficas, las unidades pueden ser grados y minutos.

4. ¿Puedo calcular el área de un triángulo si los puntos no están en el mismo plano?

No, para calcular el área de un triángulo es necesario que los tres puntos estén en el mismo plano.

5. ¿Cómo puedo comprobar que mi cálculo del área del triángulo es correcto?

Puedes comprobar tu cálculo usando diferentes métodos, como calcular el área con otra fórmula o utilizando software de geometría. También puedes comparar tu resultado con el de otra persona que haya realizado el mismo cálculo.