Como despejar la x en una ecuacion de segundo grado

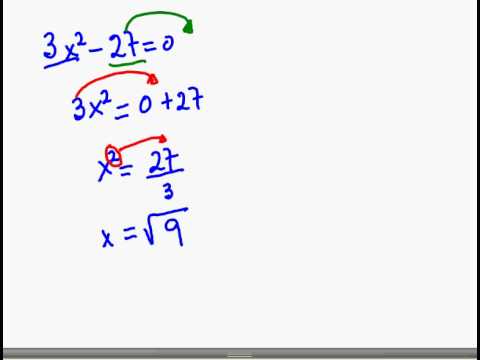
Si estás estudiando matemáticas, es muy probable que te hayas encontrado con las ecuaciones de segundo grado. Estas ecuaciones son aquellas que tienen la forma ax^2 + bx + c = 0, donde a, b y c son coeficientes conocidos y x es la incógnita que debemos despejar.

Despejar la x en una ecuación de segundo grado puede parecer una tarea complicada, pero en realidad es bastante sencillo si se sigue el procedimiento correcto. En este artículo te explicaremos paso a paso cómo despejar la x en una ecuación de segundo grado y te daremos algunos ejemplos para que lo puedas entender mejor.

Paso 1: Identificar los coeficientes a, b y c

Lo primero que debemos hacer es identificar los coeficientes a, b y c de la ecuación. Estos coeficientes se encuentran en la forma ax^2 + bx + c = 0. Por ejemplo, si tenemos la ecuación 2x^2 + 5x - 3 = 0, los coeficientes son a = 2, b = 5 y c = -3.

Paso 2: Aplicar la fórmula general

Una vez que hemos identificado los coeficientes, podemos aplicar la fórmula general para despejar la x en la ecuación de segundo grado. Esta fórmula es:

x = (-b ± sqrt(b^2 - 4ac)) / 2a

Donde sqrt significa raíz cuadrada. En otras palabras, debemos sustituir los valores de a, b y c en la fórmula y resolverla para obtener los valores de x. Es importante tener en cuenta que en algunas ocasiones puede haber más de una solución para la ecuación de segundo grado.

Paso 3: Resolver la fórmula general

Una vez que hemos aplicado la fórmula general, debemos resolverla para obtener los valores de x. En nuestro ejemplo anterior (2x^2 + 5x - 3 = 0), la fórmula general quedaría así:

x = (-5 ± sqrt(5^2 - 4(2)(-3))) / 2(2)

Resolviendo la fórmula, obtendríamos los valores de x:

x1 = (-5 + sqrt(49)) / 4 = 1/2
x2 = (-5 - sqrt(49)) / 4 = -3

Por lo tanto, las soluciones de la ecuación 2x^2 + 5x - 3 = 0 son x = 1/2 y x = -3.

Ejemplos adicionales

Veamos algunos ejemplos adicionales para que puedas entender mejor el procedimiento:

- Ecuación: x^2 - 6x + 8 = 0
- Coeficientes: a = 1, b = -6, c = 8
- Fórmula general: x = (6 ± sqrt(6^2 - 4(1)(8))) / 2(1)
- Soluciones: x1 = 4, x2 = 2

- Ecuación: 3x^2 + 2x - 1 = 0
- Coeficientes: a = 3, b = 2, c = -1
- Fórmula general: x = (-2 ± sqrt(2^2 - 4(3)(-1))) / 2(3)
- Soluciones: x1 = 1/3, x2 = -1

Conclusión

Despejar la x en una ecuación de segundo grado puede parecer complicado al principio, pero siguiendo el procedimiento correcto (identificar los coeficientes, aplicar la fórmula general y resolverla), podemos obtener las soluciones de manera sencilla. Es importante practicar con diferentes ejemplos para comprender bien el procedimiento.

Preguntas frecuentes

¿Qué es una ecuación de segundo grado?

Una ecuación de segundo grado es aquella que tiene la forma ax^2 + bx + c = 0, donde a, b y c son coeficientes conocidos y x es la incógnita que debemos despejar.

¿Por qué es importante despejar la x en una ecuación de segundo grado?

Despejar la x en una ecuación de segundo grado es importante porque nos permite encontrar las soluciones de la ecuación. Estas soluciones pueden tener aplicaciones en diferentes áreas, como la física, la ingeniería o la economía.

¿Qué es la fórmula general para despejar la x en una ecuación de segundo grado?

La fórmula general para despejar la x en una ecuación de segundo grado es x = (-b ± sqrt(b^2 - 4ac)) / 2a.

¿Puede haber más de una solución en una ecuación de segundo grado?

Sí, puede haber más de una solución en una ecuación de segundo grado. En algunos casos, puede haber dos soluciones (una positiva y otra negativa) y en otros puede haber una única solución.

¿Cómo puedo practicar para despejar la x en ecuaciones de segundo grado?

Puedes practicar resolviendo diferentes ejemplos de ecuaciones de segundo grado. También puedes buscar ejercicios en línea o en libros de matemáticas y resolverlos por tu cuenta. Recuerda que la práctica es fundamental para comprender bien el procedimiento y obtener buenos resultados.