Como saber si una funcion es creciente o decreciente derivada

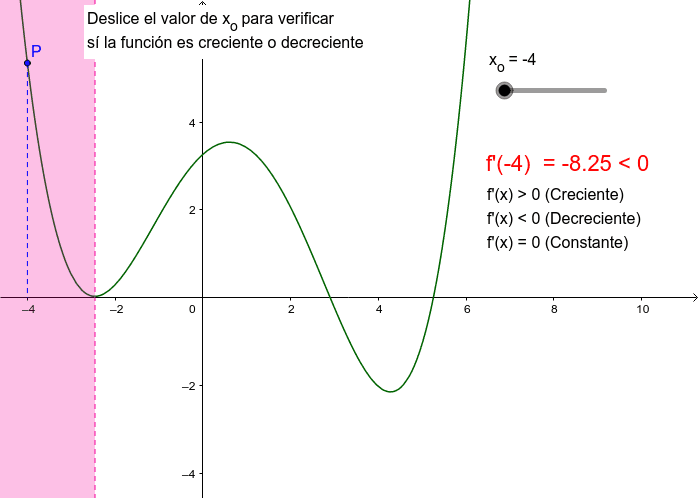
La derivada de una función es una herramienta fundamental en el cálculo diferencial e integral. La derivada de una función es la tasa de cambio instantánea de la función en un punto particular. Una función es creciente si su derivada es positiva y decreciente si su derivada es negativa. En este artículo, vamos a explorar cómo podemos usar la derivada de una función para determinar si es creciente o decreciente.

¿Qué es una función creciente?

Una función es creciente si su valor aumenta a medida que su variable independiente se incrementa. En términos matemáticos, podemos decir que la función f(x) es creciente si para cualquier par de valores de x₁ y x₂, si x₁ < x₂ entonces f(x₁) < f(x₂).Una función creciente puede visualizarse como una línea ascendente en un gráfico, donde la pendiente de la línea es siempre positiva. En otras palabras, la tasa de cambio de la función siempre es positiva.

¿Qué es una función decreciente?

Una función es decreciente si su valor disminuye a medida que su variable independiente se incrementa. En términos matemáticos, podemos decir que la función f(x) es decreciente si para cualquier par de valores de x₁ y x₂, si x₁ < x₂ entonces f(x₁) > f(x₂).

Una función decreciente puede visualizarse como una línea descendente en un gráfico, donde la pendiente de la línea es siempre negativa. En otras palabras, la tasa de cambio de la función siempre es negativa.

¿Cómo determinar si una función es creciente o decreciente usando su derivada?

La derivada de una función nos da la tasa de cambio instantánea de la función en cualquier punto dado. Si la derivada es positiva, significa que la función está creciendo en ese punto. Si la derivada es negativa, significa que la función está disminuyendo en ese punto.

Para determinar si una función es creciente o decreciente, simplemente necesitamos tomar la derivada de la función y analizar su signo. Si la derivada es positiva, la función es creciente. Si la derivada es negativa, la función es decreciente.

Ejemplo:

Consideremos la función f(x) = x². Para encontrar su derivada, tomamos la derivada de la función con respecto a x:

f'(x) = 2x

La derivada de la función es 2x. Si x es positivo, la derivada es positiva, lo que significa que la función está creciendo. Si x es negativo, la derivada es negativa, lo que significa que la función está decreciendo.

En este ejemplo, la función es creciente para todos los valores de x mayores que cero y es decreciente para todos los valores de x menores que cero.

Tabla de signos de la derivada

Una forma útil de determinar si una función es creciente o decreciente es hacer una tabla de signos de la derivada. En esta tabla, se incluyen los puntos críticos, que son los valores de x donde la función cambia de creciente a decreciente o viceversa.

Para hacer una tabla de signos de la derivada, simplemente necesitamos encontrar los puntos críticos y luego determinar el signo de la derivada en cada intervalo entre los puntos críticos.

Ejemplo:

Consideremos la función f(x) = x³ - 6x² + 9x - 2. Para encontrar los puntos críticos de la función, tomamos su derivada:

f'(x) = 3x² - 12x + 9

Para encontrar los puntos críticos, igualamos la derivada a cero y resolvemos para x:

3x² - 12x + 9 = 0
x² - 4x + 3 = 0
(x - 3)(x - 1) = 0

Los puntos críticos de la función son x = 1 y x = 3. Luego, hacemos una tabla de signos de la derivada:

| Intervalo | Signo de f'(x) |
|-----------|----------------|
| (-∞,1) | + |
| (1,3) | - |
| (3,∞) | + |

En este ejemplo, la función es creciente en el intervalo (-∞,1) y (3,∞) y es decreciente en el intervalo (1,3).

Conclusión

En resumen, La derivada de una función nos da la tasa de cambio instantánea de la función en cualquier punto dado. Si la derivada es positiva, significa que la función está creciendo en ese punto. Si la derivada es negativa, significa que la función está disminuyendo en ese punto. Para determinar si una función es creciente o decreciente, simplemente necesitamos tomar la derivada de la función y analizar su signo. Si la derivada es positiva, la función es creciente. Si la derivada es negativa, la función es decreciente.

Preguntas frecuentes

¿Qué es una función creciente?

Una función es creciente si su valor aumenta a medida que su variable independiente se incrementa.

¿Qué es una función decreciente?

Una función es decreciente si su valor disminuye a medida que su variable independiente se incrementa.

¿Qué es la derivada de una función?

La derivada de una función es la tasa de cambio instantánea de la función en un punto particular.

¿Cómo se encuentra la derivada de una función?

La derivada de una función se encuentra tomando la derivada de la función con respecto a su variable independiente.

¿Qué son los puntos críticos de una función?

Los puntos críticos de una función son los valores de x donde la función cambia de creciente a decreciente o viceversa.