Como saber si una funcion es integrable en un intervalo

Si estás estudiando cálculo o matemáticas avanzadas, seguramente te has encontrado con el concepto de integración. La integración es una herramienta matemática muy poderosa que se utiliza para calcular áreas, volúmenes, trabajo y muchas otras cosas. Pero, ¿cómo saber si una función es integrable en un intervalo? En este artículo te explicaremos todo lo que necesitas saber al respecto.

¿Qué es la integración?

Antes de entrar en materia, es importante que tengamos claro qué es la integración. En términos simples, la integración es el proceso que nos permite calcular el área bajo una curva en un intervalo dado. Esta área se puede interpretar como el trabajo realizado por una fuerza que varía con el tiempo o como la cantidad de líquido que fluye a través de un tubo en un tiempo determinado.

¿Qué es una función integrable?

Una función integrable es aquella que se puede integrar en un intervalo determinado. En otras palabras, si una función es integrable en un intervalo, entonces podemos calcular el área bajo su curva en ese intervalo.

Sin embargo, no todas las funciones son integrables. Hay algunas funciones que son demasiado complejas para ser integradas analíticamente (es decir, mediante fórmulas matemáticas). En estos casos, es necesario utilizar métodos numéricos para aproximar la integral.

Criterios de integrabilidad de una función

Existen varios criterios que nos permiten determinar si una función es integrable en un intervalo o no. A continuación, te presentamos algunos de los más comunes:

Criterio de Riemann

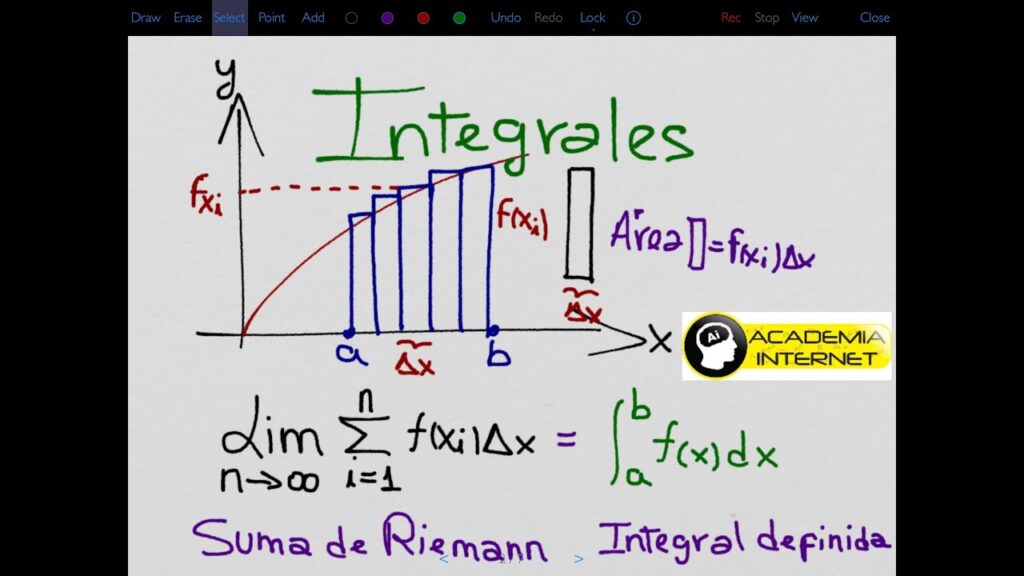
El criterio de Riemann establece que una función es integrable en un intervalo [a, b] si y solo si la suma de Riemann converge a un número finito cuando el tamaño de los subintervalos se acerca a cero. La suma de Riemann se define como:

$$sum_{i=1}^{n}f(c_i)Delta x_i$$

donde $c_i$ es un punto cualquiera en el subintervalo $[x_{i-1},x_i]$ y $Delta x_i$ es la longitud del subintervalo.

En otras palabras, si la suma de Riemann converge a un número finito cuando hacemos los subintervalos cada vez más pequeños, entonces la función es integrable en el intervalo [a, b].

Criterio de Lebesgue

El criterio de Lebesgue establece que una función es integrable en un intervalo [a, b] si y solo si su función de variación acotada. La función de variación se define como:

$$V_a^bf(x) = sup sum_{i=1}^{n} |f(x_i)-f(x_{i-1})|$$

donde el supremo se toma sobre todas las particiones finitas del intervalo [a, b].

En otras palabras, si la función de variación es acotada en el intervalo [a, b], entonces la función es integrable en ese intervalo.

Criterio de Cauchy

El criterio de Cauchy establece que una función es integrable en un intervalo [a, b] si y solo si, para cualquier número positivo $epsilon$, existe una partición finita del intervalo tal que la suma de Riemann para cualquier partición refinada difiere menos de $epsilon$. En otras palabras, si podemos hacer la suma de Riemann tan cercana como queramos a un número finito mediante particiones suficientemente finas, entonces la función es integrable en el intervalo.

Conclusiones

En resumen, Saber si una función es integrable en un intervalo es un problema importante en matemáticas. Existen varios criterios que nos permiten determinar si una función es integrable o no, como el criterio de Riemann, el criterio de Lebesgue y el criterio de Cauchy. Estos criterios nos permiten trabajar con funciones complejas y calcular áreas, volúmenes y otros objetos matemáticos importantes.

Preguntas frecuentes

¿Por qué es importante saber si una función es integrable?

Saber si una función es integrable es importante porque nos permite calcular áreas, volúmenes, trabajo y muchas otras cosas. La integración es una herramienta matemática muy poderosa que se utiliza en muchas áreas de la ciencia y la ingeniería.

¿Cómo se calcula la integral de una función?

Existen diferentes técnicas para calcular la integral de una función, como la integración por sustitución, la integración por partes y la integración por fracciones parciales. Cada técnica se utiliza según las características de la función que se quiera integrar.

¿Qué es una integral definida?

Una integral definida es una integral que se calcula en un intervalo específico, es decir, que tiene un límite inferior y un límite superior. La integral definida se representa mediante el símbolo $int_{a}^{b}f(x)dx$ y representa el área bajo la curva de la función $f(x)$ en el intervalo [a, b].

¿Qué es la regla del trapecio?

La regla del trapecio es un método numérico para aproximar la integral de una función. Consiste en aproximar el área bajo la curva mediante la suma de las áreas de los trapecios que se forman al unir los puntos de la función con los ejes $x$ y $y$. Este método es útil cuando la función que se quiere integrar es muy compleja para ser integrada analíticamente.

¿Qué son las tablas de integrales?

Las tablas de integrales son herramientas matemáticas que contienen las fórmulas de las integrales de muchas funciones comunes. Estas tablas son muy útiles para resolver problemas de integrales y para verificar los resultados de los cálculos.