Como sacar el valor de dos incognitas en una ecuacion

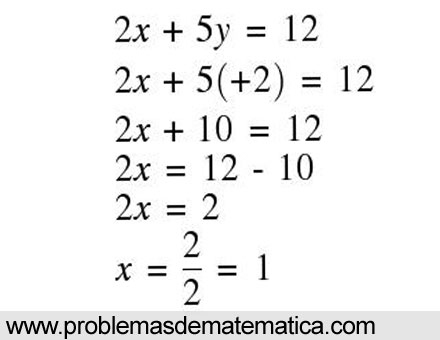
Las ecuaciones son una parte fundamental de las matemáticas y se utilizan para resolver problemas en una variedad de campos, desde la física hasta la economía. En una ecuación, las incógnitas son los valores desconocidos que se deben encontrar para resolver la ecuación. A menudo, las ecuaciones tienen solo una incógnita, pero en algunos casos, pueden tener dos incógnitas. En este artículo, vamos a explorar cómo sacar el valor de dos incógnitas en una ecuación.

¿Qué son las incógnitas en una ecuación?

Las incógnitas son los valores desconocidos que se deben encontrar para resolver una ecuación. Por ejemplo, en la ecuación "2x + 3 = 7", la incógnita es "x". Para resolver la ecuación, se debe encontrar el valor de "x" que hace que la ecuación sea verdadera.

¿Qué son las ecuaciones con dos incógnitas?

Las ecuaciones con dos incógnitas son ecuaciones que tienen dos valores desconocidos que se deben encontrar para resolver la ecuación. Por ejemplo, la ecuación "2x + 3y = 10" tiene dos incógnitas, "x" y "y". Para resolver la ecuación, se debe encontrar el valor de "x" y "y" que hacen que la ecuación sea verdadera.

¿Cómo se resuelven las ecuaciones con dos incógnitas?

Para resolver una ecuación con dos incógnitas, se necesitan dos ecuaciones que contengan las mismas incógnitas. Esto se conoce como un sistema de ecuaciones. Por ejemplo, si tenemos las ecuaciones "2x + 3y = 10" y "4x - y = 5", podemos resolver el sistema de ecuaciones para encontrar los valores de "x" y "y" que hacen que ambas ecuaciones sean verdaderas.

Existen varias formas de resolver un sistema de ecuaciones, pero una de las más comunes es el método de sustitución. En este método, se despeja una de las incógnitas de una de las ecuaciones y se sustituye en la otra ecuación. Luego, se resuelve la ecuación resultante para encontrar el valor de la otra incógnita. Finalmente, se sustituyen los valores encontrados en una de las ecuaciones originales para encontrar el valor de la otra incógnita.

Ejemplo de cómo sacar el valor de dos incógnitas en una ecuación:

Para ilustrar cómo se resuelven las ecuaciones con dos incógnitas, consideremos el siguiente sistema de ecuaciones:

2x + y = 5
x - y = 1

Para resolver este sistema de ecuaciones, primero despejamos "y" de la segunda ecuación:

x - y = 1
-y = -x + 1
y = x - 1

Luego, sustituimos esta expresión para "y" en la primera ecuación:

2x + y = 5
2x + (x - 1) = 5
3x - 1 = 5
3x = 6
x = 2

Finalmente, sustituimos este valor de "x" en la expresión que encontramos para "y":

y = x - 1
y = 2 - 1
y = 1

Por lo tanto, la solución del sistema de ecuaciones es "x = 2" e "y = 1".

Conclusión:

Las ecuaciones con dos incógnitas son una parte importante de las matemáticas y se utilizan para resolver problemas en una variedad de campos. Para resolver una ecuación con dos incógnitas, se necesitan dos ecuaciones que contengan las mismas incógnitas. Luego, se puede utilizar el método de sustitución para encontrar los valores de las incógnitas.

Preguntas frecuentes:

1. ¿Las ecuaciones con dos incógnitas siempre tienen una solución?

No necesariamente. Algunas ecuaciones con dos incógnitas no tienen solución, mientras que otras tienen infinitas soluciones.

2. ¿Qué sucede si las dos ecuaciones en un sistema de ecuaciones son iguales?

Si las dos ecuaciones en un sistema de ecuaciones son iguales, entonces hay infinitas soluciones.

3. ¿Cómo puedo saber si un sistema de ecuaciones tiene solución única?

Un sistema de ecuaciones tiene solución única si las dos ecuaciones no son múltiplos uno del otro.

4. ¿Qué es el método de eliminación para resolver sistemas de ecuaciones?

El método de eliminación es otro método para resolver sistemas de ecuaciones. En este método, se suman o restan las dos ecuaciones para eliminar una de las incógnitas y luego se resuelve la ecuación resultante para encontrar el valor de la otra incógnita.

5. ¿Cómo puedo comprobar si mis soluciones son correctas?

Para comprobar si las soluciones son correctas, simplemente sustituye los valores encontrados en ambas ecuaciones originales y comprueba si ambas ecuaciones son verdaderas. Si ambas ecuaciones son verdaderas, entonces las soluciones son correctas.