Como se llama el punto de interseccion de las alturas
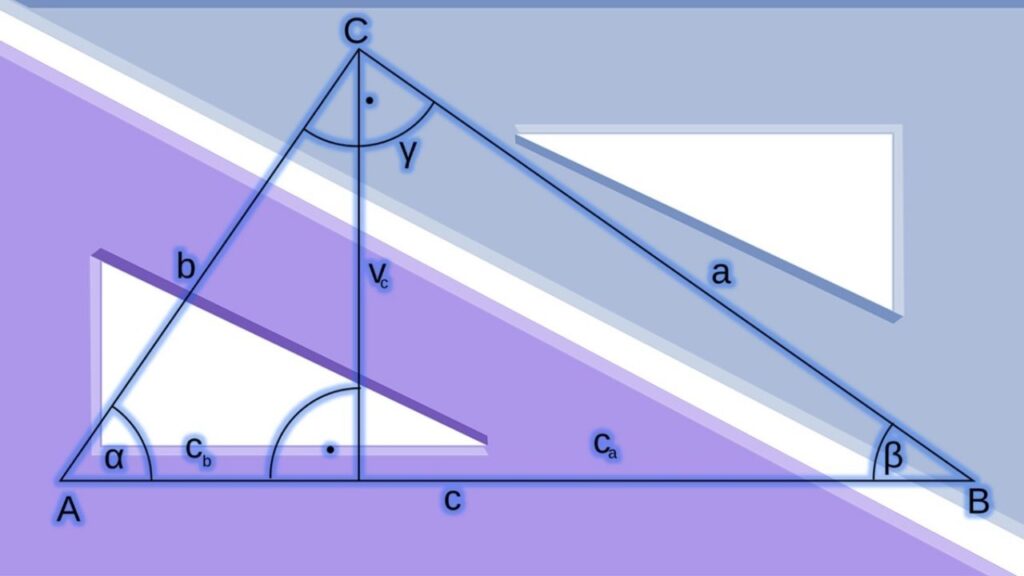
Si alguna vez has estudiado geometría, probablemente hayas oído hablar de las alturas de un triángulo. Las alturas son líneas que se extienden desde cada vértice del triángulo hasta el lado opuesto, formando ángulos rectos. Pero, ¿sabes cómo se llama el punto donde se intersectan todas las alturas?
El punto de intersección de las alturas de un triángulo se llama Ortocentro. El ortocentro es un punto muy importante en la geometría del triángulo ya que tiene muchas propiedades interesantes.
¿Cómo encontrar el Ortocentro?
Existen varias formas de encontrar el Ortocentro de un triángulo, pero aquí te presentamos dos de las más comunes:
Método 1:
1. Dibuja un triángulo y traza las alturas desde cada uno de los vértices.
2. Las alturas se intersectarán en un punto. Ese punto es el Ortocentro.
Método 2:
1. Encuentra las coordenadas de los tres vértices del triángulo.
2. Encuentra las ecuaciones de las tres rectas que contienen cada lado del triángulo.
3. Encuentra las ecuaciones de las tres rectas perpendiculares a cada una de las tres rectas del paso anterior que pasan por cada uno de los vértices del triángulo.
4. Encuentra los puntos de intersección de cada una de las tres rectas perpendiculares encontradas en el paso anterior.
5. El punto de intersección de las tres rectas perpendiculares encontradas en el paso anterior es el Ortocentro.
Propiedades del Ortocentro
El Ortocentro tiene varias propiedades interesantes, algunas de las cuales se detallan a continuación:
- El Ortocentro siempre está dentro del triángulo, excepto en el caso del triángulo equilátero, donde el Ortocentro es el mismo punto que el Circuncentro y el Baricentro.
- El Ortocentro es el punto donde la suma de las distancias desde cada vértice del triángulo a su respectiva altura es mínima.
- El Ortocentro es el punto donde la distancia desde cada vértice del triángulo a su respectiva altura es igual.
- El Ortocentro es el punto donde las bisectrices de los ángulos internos del triángulo se intersectan, formando el llamado "circuncentro de los ángulos".
- El Ortocentro es el punto donde las diagonales del cuadrilátero formado por las proyecciones de los vértices del triángulo sobre su lado opuesto se intersectan.
Comparación con tablas
Una forma de comparar el Ortocentro con otras propiedades de los triángulos es mediante el uso de tablas. En la siguiente tabla, se comparan las propiedades del Ortocentro con las del Circuncentro y el Baricentro:
| Propiedad | Ortocentro | Circuncentro | Baricentro |
|---|---|---|---|
| Siempre está dentro del triángulo | Sí | Sí | Sí |
| Suma de las distancias vértice-altura es mínima | Sí | No | No |
| Distancia vértice-altura es igual | Sí | No | No |
| Bisectrices de los ángulos se intersectan | Sí | Sí | No |
| Diagonales del cuadrilátero formado por las proyecciones de los vértices del triángulo sobre su lado opuesto se intersectan | Sí | No | No |
Preguntas Frecuentes
¿El Ortocentro siempre está dentro del triángulo?
Sí, excepto en el caso del triángulo equilátero, donde el Ortocentro es el mismo punto que el Circuncentro y el Baricentro.
¿Cómo se encuentra el Ortocentro?
Existen varias formas de encontrar el Ortocentro de un triángulo, pero dos de las más comunes son trazar las alturas desde cada vértice del triángulo o utilizar las coordenadas de los vértices del triángulo y las ecuaciones de las rectas que contienen cada lado del triángulo.
¿Qué propiedades tiene el Ortocentro?
El Ortocentro tiene varias propiedades interesantes, como ser el punto donde la suma de las distancias desde cada vértice del triángulo a su respectiva altura es mínima, el punto donde las bisectrices de los ángulos internos del triángulo se intersectan y el punto donde las diagonales del cuadrilátero formado por las proyecciones de los vértices del triángulo sobre su lado opuesto se intersectan.
¿Cómo se compara el Ortocentro con otras propiedades de los triángulos?
Una forma de comparar el Ortocentro con otras propiedades de los triángulos es mediante el uso de tablas, como se muestra en este artículo.
¿El Ortocentro es útil en la vida real?
Aunque no es una propiedad que se utilice a menudo en la vida diaria, el Ortocentro es un concepto importante en matemáticas y geometría y puede ser útil en campos como la ingeniería y la arquitectura. Además, es un tema importante en la educación matemática y puede ayudar a desarrollar la capacidad de razonamiento y solución de problemas.

Deja una respuesta