Cuando un sistema de ecuaciones lineales 2x2 tiene infinitas soluciones

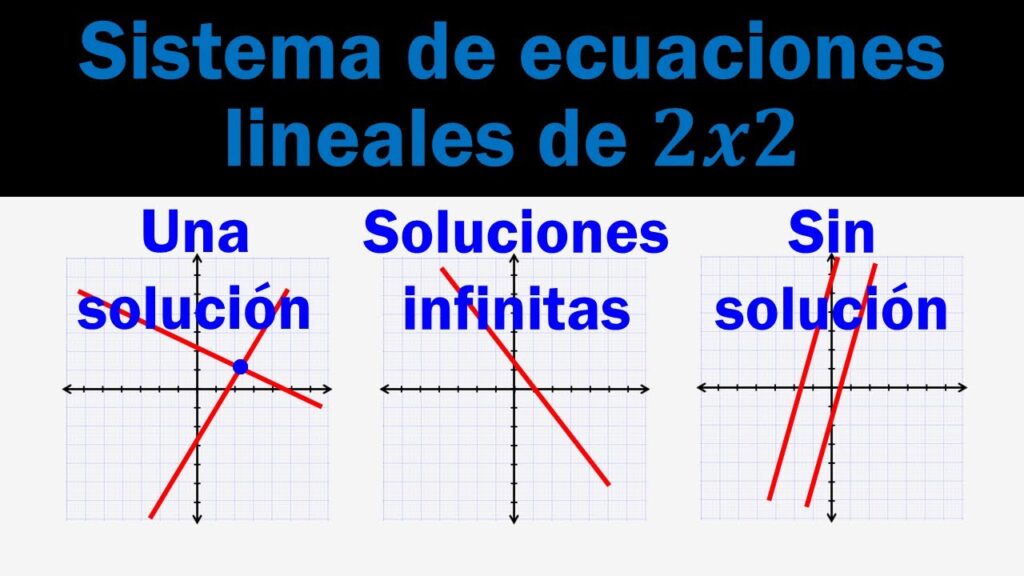
Un sistema de ecuaciones lineales 2x2 es un conjunto de dos ecuaciones lineales con dos incógnitas. Si las ecuaciones son independientes, entonces el sistema tiene una solución única. Si las ecuaciones son dependientes, entonces el sistema tiene infinitas soluciones. En este artículo, nos enfocaremos en el caso en el que el sistema tiene infinitas soluciones y analizaremos cuándo sucede esto y cómo encontrar todas las soluciones.

¿Qué significa que un sistema tenga infinitas soluciones?

Cuando un sistema de ecuaciones lineales 2x2 tiene infinitas soluciones, significa que hay una familia completa de soluciones que satisfacen ambas ecuaciones. Esto se puede entender como una línea en el plano que contiene todas las soluciones posibles del sistema.

Un ejemplo sencillo

Para ilustrar este concepto, consideremos el siguiente sistema de ecuaciones:

x + y = 3

2x + 2y = 6

Podemos notar que la segunda ecuación es simplemente la primera multiplicada por 2. Por lo tanto, estas ecuaciones son dependientes y tienen infinitas soluciones. Para encontrarlas, podemos despejar y en la primera ecuación:

y = 3 - x

Luego, podemos sustituir esta expresión en la segunda ecuación:

2x + 2(3 - x) = 6

Simplificando, obtenemos:

x = 1

Sustituyendo este valor en la expresión que encontramos para y, obtenemos:

y = 2

Por lo tanto, la solución única del sistema es (1, 2). Sin embargo, también podemos expresar todas las soluciones del sistema en términos de un parámetro t:

x = t

y = 3 - t

Esto significa que cualquier par (t, 3 - t) es una solución del sistema. En otras palabras, hay una línea en el plano que contiene todas las soluciones posibles.

Cuándo un sistema tiene infinitas soluciones

Un sistema de ecuaciones lineales 2x2 tiene infinitas soluciones si y solo si las dos ecuaciones son linealmente dependientes. Esto significa que una de las ecuaciones puede obtenerse multiplicando la otra por una constante diferente de cero. En términos geométricos, esto significa que las dos ecuaciones representan rectas paralelas o la misma recta.

Un ejemplo un poco más complicado

Consideremos el siguiente sistema de ecuaciones:

3x - 2y = 1

9x - 6y = 3

Podemos notar que la segunda ecuación es simplemente la primera multiplicada por 3. Por lo tanto, estas ecuaciones son dependientes y tienen infinitas soluciones. Para encontrarlas, podemos despejar y en la primera ecuación:

y = (3x - 1)/2

Luego, podemos sustituir esta expresión en la segunda ecuación:

9x - 6[(3x - 1)/2] = 3

Simplificando, obtenemos:

x = 1

Sustituyendo este valor en la expresión que encontramos para y, obtenemos:

y = 1

Por lo tanto, la solución única del sistema es (1, 1). Sin embargo, también podemos expresar todas las soluciones del sistema en términos de un parámetro t:

x = t

y = (3t - 1)/2

Esto significa que cualquier par (t, (3t - 1)/2) es una solución del sistema. En otras palabras, hay una línea en el plano que contiene todas las soluciones posibles.

Conclusión

En resumen, Un sistema de ecuaciones lineales 2x2 tiene infinitas soluciones si las dos ecuaciones son linealmente dependientes. Esto significa que una de las ecuaciones puede obtenerse multiplicando la otra por una constante diferente de cero. En términos geométricos, esto significa que las dos ecuaciones representan rectas paralelas o la misma recta. Para encontrar todas las soluciones del sistema, podemos expresarlas en términos de un parámetro.

Preguntas frecuentes

1. ¿Qué significa que un sistema tenga una solución única?

Un sistema de ecuaciones lineales 2x2 tiene una solución única si las dos ecuaciones son independientes. Esto significa que no hay una relación lineal entre ellas y representan dos rectas que se intersectan en un punto en el plano.

2. ¿Por qué es importante saber si un sistema tiene infinitas soluciones?

Saber si un sistema de ecuaciones lineales 2x2 tiene infinitas soluciones es importante porque nos permite entender mejor la geometría del problema que estamos resolviendo. Además, nos permite encontrar todas las soluciones posibles del sistema.

3. ¿Cómo se puede determinar si un sistema tiene una solución única o infinitas soluciones?

Para determinar si un sistema de ecuaciones lineales 2x2 tiene una solución única o infinitas soluciones, podemos utilizar el método de eliminación o el método de sustitución. Si al aplicar cualquiera de estos métodos encontramos una única solución, entonces el sistema tiene una solución única. Si encontramos una expresión en términos de un parámetro, entonces el sistema tiene infinitas soluciones.

4. ¿Cómo se puede representar geométricamente un sistema con infinitas soluciones?

Un sistema de ecuaciones lineales 2x2 con infinitas soluciones puede representarse geométricamente como una línea en el plano que contiene todas las soluciones posibles del sistema.

5. ¿Por qué es importante saber cómo encontrar todas las soluciones de un sistema con infinitas soluciones?

Saber cómo encontrar todas las soluciones de un sistema de ecuaciones lineales 2x2 con infinitas soluciones es importante porque nos permite entender mejor la geometría del problema que estamos resolviendo y nos permite encontrar todas las soluciones posibles del sistema. Esto puede tener aplicaciones prácticas en áreas como la física, la ingeniería y la economía.