Determina el valor de los angulos interiores del triangulo abc
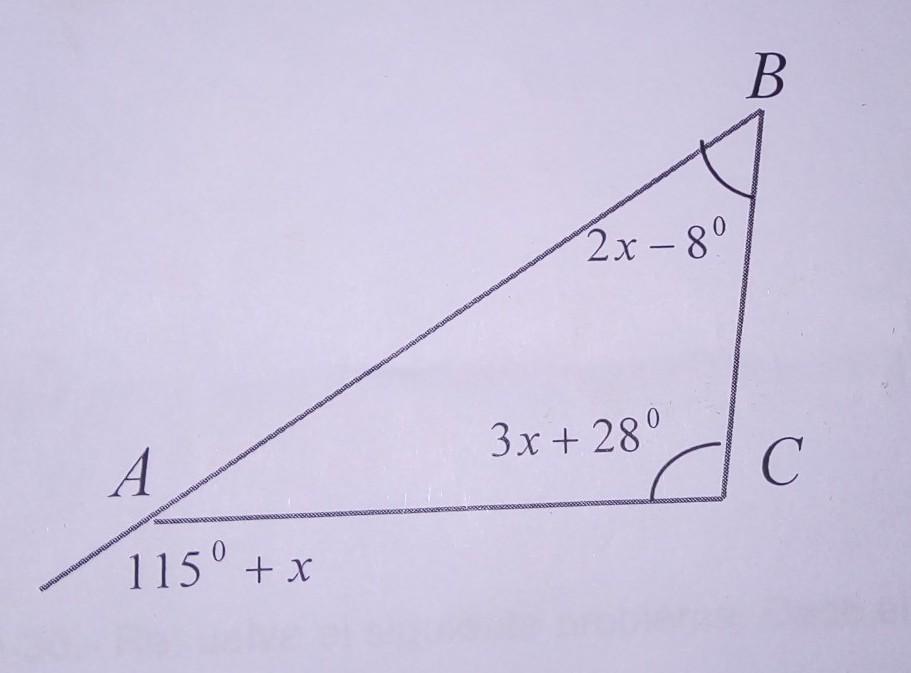
Los ángulos interiores de un triángulo son uno de los conceptos fundamentales de la geometría. En este artículo, explicaremos cómo determinar el valor de los ángulos interiores de un triángulo ABC. Pero antes de profundizar en este tema, es importante entender algunos conceptos básicos.
- Conceptos básicos de los ángulos en un triángulo
- Cómo determinar los ángulos interiores de un triángulo
- Usando la ley de cosenos y la ley de senos
- Comparación con tablas
- Preguntas frecuentes
- ¿Qué es un triángulo?
- ¿Cómo se calcula la suma de los ángulos interiores de un triángulo?
- ¿Cómo se clasifican los triángulos según la medida de sus ángulos interiores?
- ¿Cómo se determina un ángulo desconocido en un triángulo?
- ¿Cómo se utilizan la ley de cosenos y la ley de senos para determinar los ángulos interiores de un triángulo?
Conceptos básicos de los ángulos en un triángulo
Un triángulo es una figura geométrica que consta de tres lados y tres ángulos. La suma de los ángulos interiores de un triángulo siempre es igual a 180 grados. Esto significa que si conocemos dos de los ángulos interiores de un triángulo, podemos encontrar el tercer ángulo simplemente restando la suma de los otros dos ángulos de 180 grados.
Además, los triángulos se clasifican de acuerdo con la medida de sus ángulos interiores. Un triángulo rectángulo tiene un ángulo recto (90 grados), mientras que un triángulo agudo tiene tres ángulos agudos (menos de 90 grados). Por otro lado, un triángulo obtuso tiene un ángulo obtuso (más de 90 grados).
Cómo determinar los ángulos interiores de un triángulo
Para determinar los ángulos interiores de un triángulo, necesitamos conocer al menos dos de los ángulos. A partir de ahí, podemos encontrar el tercer ángulo utilizando la fórmula de la suma de los ángulos interiores.
Por ejemplo, supongamos que conocemos dos ángulos interiores de un triángulo ABC. El ángulo A mide 50 grados, mientras que el ángulo B mide 60 grados. Para encontrar el tercer ángulo, simplemente restamos la suma de los otros dos ángulos de 180 grados:
Ángulo C = 180 grados - (50 grados + 60 grados)
Ángulo C = 70 grados
Por lo tanto, el ángulo C mide 70 grados.
Usando la ley de cosenos y la ley de senos
Otra forma de determinar los ángulos interiores de un triángulo es utilizando la ley de cosenos y la ley de senos. Estas leyes son útiles cuando conocemos los tres lados del triángulo pero no conocemos ninguno de los ángulos.
La ley de cosenos establece que el cuadrado de un lado de un triángulo es igual a la suma de los cuadrados de los otros dos lados menos el doble del producto de esos dos lados y el coseno del ángulo opuesto al primer lado. La ley de senos establece que la longitud de un lado de un triángulo está en proporción directa con el seno del ángulo opuesto.
Por ejemplo, si conocemos los tres lados de un triángulo ABC (a, b y c), podemos encontrar el ángulo opuesto al lado a utilizando la ley de cosenos:
cos A = (b^2 + c^2 - a^2) / (2bc)
Luego podemos usar la ley de senos para encontrar los otros dos ángulos:
sin B = (b * sin A) / a
sin C = (c * sin A) / a
Comparación con tablas
Para visualizar mejor los ángulos interiores de un triángulo, podemos utilizar tablas. Por ejemplo, podemos crear una tabla que muestre los tres ángulos interiores de un triángulo y su clasificación según la medida de los ángulos.
| Ángulo | Clasificación |
|---|---|
| Menos de 90 grados | Triángulo agudo |
| 90 grados | Triángulo rectángulo |
| Más de 90 grados | Triángulo obtuso |
Preguntas frecuentes
¿Qué es un triángulo?
Un triángulo es una figura geométrica que consta de tres lados y tres ángulos.
¿Cómo se calcula la suma de los ángulos interiores de un triángulo?
La suma de los ángulos interiores de un triángulo siempre es igual a 180 grados.
¿Cómo se clasifican los triángulos según la medida de sus ángulos interiores?
Los triángulos se clasifican como agudos (menos de 90 grados), rectángulos (90 grados) u obtusos (más de 90 grados).
¿Cómo se determina un ángulo desconocido en un triángulo?
Para determinar un ángulo desconocido en un triángulo, necesitamos conocer al menos dos de los ángulos interiores. A partir de ahí, podemos encontrar el tercer ángulo utilizando la fórmula de la suma de los ángulos interiores.
¿Cómo se utilizan la ley de cosenos y la ley de senos para determinar los ángulos interiores de un triángulo?
La ley de cosenos establece que el cuadrado de un lado de un triángulo es igual a la suma de los cuadrados de los otros dos lados menos el doble del producto de esos dos lados y el coseno del ángulo opuesto al primer lado. La ley de senos establece que la longitud de un lado de un triángulo está en proporción directa con el seno del ángulo opuesto.

Deja una respuesta