Ecuaciones con dos o tres incognitas solucion grafica y matematica
Cuando hablamos de ecuaciones, normalmente pensamos en una variable y un resultado. Pero ¿qué pasa cuando tenemos más de una variable? ¿Cómo podemos resolver una ecuación con dos o tres incógnitas? En este artículo, te explicaremos cómo resolver este tipo de ecuaciones tanto gráficamente como matemáticamente.
- ¿Qué es una ecuación con dos o tres incógnitas?
- Solución gráfica de ecuaciones con dos o tres incógnitas
- Solución matemática de ecuaciones con dos o tres incógnitas
- Preguntas frecuentes
- 1. ¿Por qué es importante resolver ecuaciones con dos o tres incógnitas?
- 2. ¿Cuál es la diferencia entre una ecuación con dos incógnitas y una ecuación con tres incógnitas?
- 3. ¿Qué método es mejor para resolver ecuaciones con dos o tres incógnitas?
- 4. ¿Puedo resolver una ecuación con más de tres incógnitas?
- 5. ¿Las ecuaciones con dos o tres incógnitas solo se utilizan en la física?
¿Qué es una ecuación con dos o tres incógnitas?
Una ecuación con dos o tres incógnitas es una ecuación que tiene más de una variable desconocida. Por ejemplo:
2x + 3y = 10
En esta ecuación, tenemos dos incógnitas: x e y. Si tuviéramos una ecuación con tres incógnitas, tendríamos una tercera variable desconocida.
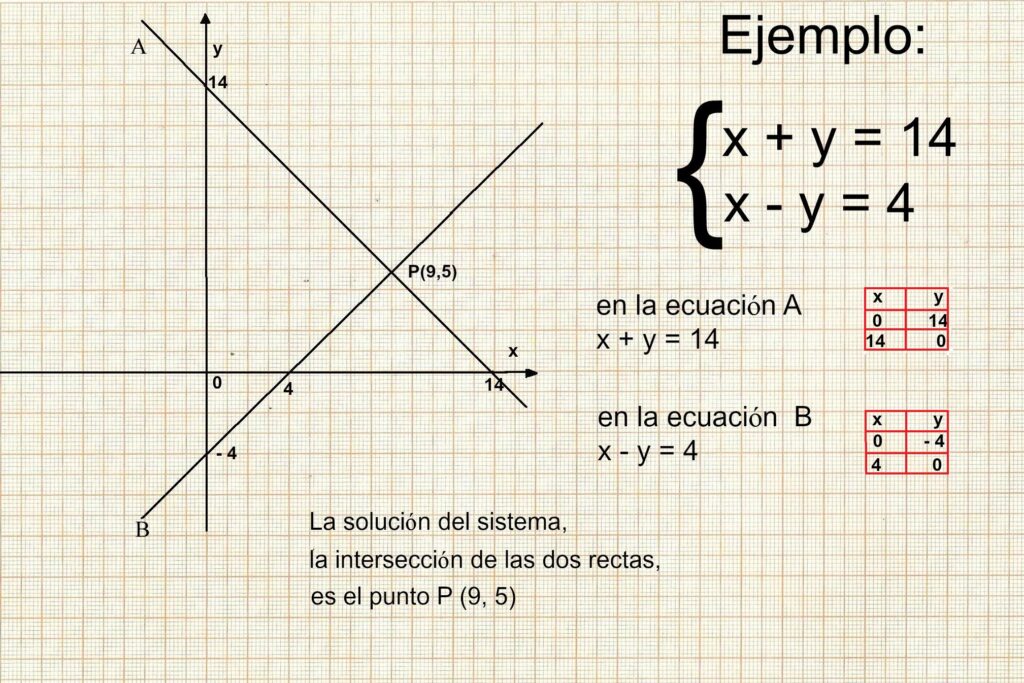
Solución gráfica de ecuaciones con dos o tres incógnitas
La solución gráfica de una ecuación con dos o tres incógnitas implica la representación de la ecuación en un plano cartesiano. Para ello, es necesario despejar una de las variables en términos de la otra. Por ejemplo, si tenemos la ecuación:
2x + 3y = 10
Podemos despejar y en términos de x:
y = (10 - 2x) / 3
Para representar esta ecuación en un plano cartesiano, dibujamos una recta con pendiente (-2/3) y una intersección con el eje y de (10/3). La solución de la ecuación será el punto donde se cruzan las rectas correspondientes a cada una de las incógnitas.
Si tenemos una ecuación con tres incógnitas, necesitamos representarla en un espacio tridimensional. Para ello, despejamos una de las variables en términos de las otras dos. Por ejemplo, si tenemos la ecuación:
x + y + z = 5
Podemos despejar z en términos de x e y:
z = 5 - x - y
Para representar esta ecuación en un espacio tridimensional, dibujamos un plano con una intersección con el eje z de (5), y una pendiente de (-1) para x y (-1) para y. La solución de la ecuación será el punto donde se cruzan los planos correspondientes a cada una de las incógnitas.
Solución matemática de ecuaciones con dos o tres incógnitas
La solución matemática de una ecuación con dos o tres incógnitas implica el uso de técnicas algebraicas para resolver el sistema de ecuaciones simultáneas. Por ejemplo, si tenemos el siguiente sistema de ecuaciones:
2x + 3y = 10
3x - 4y = -5
Podemos resolverlo utilizando el método de sustitución o el método de eliminación. En el método de sustitución, despejamos una de las variables en términos de la otra y la sustituimos en la otra ecuación. En este caso, podemos despejar y en términos de x en la primera ecuación:
y = (10 - 2x) / 3
Y sustituimos en la segunda ecuación:
3x - 4((10 - 2x) / 3) = -5
Resolviendo esta ecuación, obtenemos el valor de x. Luego, podemos sustituir este valor en cualquiera de las dos ecuaciones para obtener el valor de y.
En el método de eliminación, multiplicamos una de las ecuaciones por un número para hacer que una de las variables se cancelen entre sí. Por ejemplo, si multiplicamos la primera ecuación por 4 y la segunda ecuación por 3, obtenemos:
8x + 12y = 40
9x - 12y = -15
Sumando estas dos ecuaciones, obtenemos:
17x = 25
Y resolviendo esta ecuación, obtenemos el valor de x. Luego, podemos sustituir este valor en cualquiera de las dos ecuaciones para obtener el valor de y.
Si tenemos una ecuación con tres incógnitas, necesitamos resolver un sistema de tres ecuaciones simultáneas utilizando el mismo método de sustitución o eliminación.
Tabla comparativa de solución gráfica y matemática
A continuación, se presenta una tabla comparativa entre la solución gráfica y matemática de una ecuación con dos o tres incógnitas:
| Solución gráfica | Solución matemática |
|---|---|
| Representación en un plano cartesiano o un espacio tridimensional | Resolución de un sistema de ecuaciones simultáneas utilizando técnicas algebraicas |
| Visualización de la solución | Obtención de valores numéricos para cada una de las incógnitas |
| Requiere habilidades gráficas | Requiere habilidades algebraicas |
Preguntas frecuentes
1. ¿Por qué es importante resolver ecuaciones con dos o tres incógnitas?
Las ecuaciones con dos o tres incógnitas son útiles en situaciones donde hay más de una variable que afecta un resultado. Por ejemplo, en la física, podemos tener ecuaciones con dos o tres incógnitas que representan la posición, velocidad y aceleración de un objeto en movimiento.
2. ¿Cuál es la diferencia entre una ecuación con dos incógnitas y una ecuación con tres incógnitas?
La principal diferencia es que una ecuación con tres incógnitas necesita ser representada en un espacio tridimensional, mientras que una ecuación con dos incógnitas se representa en un plano cartesiano.
3. ¿Qué método es mejor para resolver ecuaciones con dos o tres incógnitas?
No hay un método mejor que otro, depende de la situación y de las habilidades del que resuelve la ecuación. En algunos casos, la solución gráfica puede ser más fácil y útil, mientras que en otros casos, la solución matemática puede ser más precisa.
4. ¿Puedo resolver una ecuación con más de tres incógnitas?
Sí, pero la representación gráfica puede ser más difícil. En este caso, es necesario resolver un sistema de ecuaciones simultáneas utilizando técnicas algebraicas.
5. ¿Las ecuaciones con dos o tres incógnitas solo se utilizan en la física?
No, las ecuaciones con dos o tres incógnitas se utilizan en muchas áreas, como la economía, la ingeniería, la biología, entre otras. Son útiles en cualquier situación donde hay más de una variable que afecta un resultado.

Deja una respuesta