En cual intervalo la funcion de la grafica es creciente
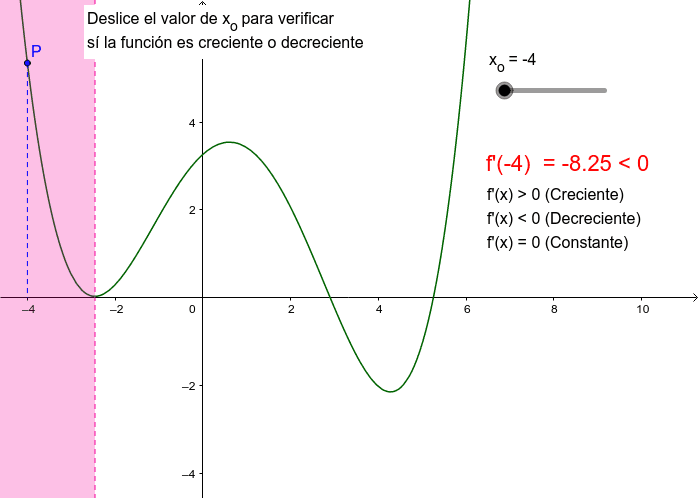
La creciente popularidad de la ciencia y la tecnología en el mundo moderno ha llevado a un mayor interés en las matemáticas y su aplicación en la vida diaria. Uno de los conceptos más importantes en matemáticas es la noción de una función creciente, que se refiere a una función cuyo valor aumenta a medida que su entrada aumenta. En este artículo, exploraremos en qué intervalo una función de la gráfica es creciente.
¿Qué es una función creciente?
Antes de poder determinar en qué intervalo una función de la gráfica es creciente, es importante entender qué es exactamente una función creciente. Una función se considera creciente si su valor aumenta a medida que su entrada aumenta. En otras palabras, si aumentamos el valor de x en una función creciente f(x), entonces el valor de f(x) también aumentará.
Por ejemplo, si tenemos una función f(x) = 2x, y evaluamos f(x) en x = 1, obtenemos f(1) = 2. Si luego evaluamos f(x) en x = 2, obtenemos f(2) = 4. Como podemos ver, el valor de la función aumenta a medida que aumentamos el valor de x, lo que significa que esta función es creciente.
En qué intervalo la función de la gráfica es creciente
Ahora que tenemos una comprensión básica de lo que es una función creciente, podemos comenzar a explorar en qué intervalo una función de la gráfica es creciente. Para hacer esto, necesitamos examinar la gráfica de la función y buscar regiones donde la función está aumentando a medida que x aumenta.
Por ejemplo, consideremos la función f(x) = x^2. Si graficamos esta función, obtenemos una parábola que se abre hacia arriba. En este caso, la función es creciente en el intervalo [0, ∞), lo que significa que a medida que x aumenta desde cero, el valor de la función también aumenta.
En general, podemos determinar en qué intervalo una función de la gráfica es creciente al examinar la pendiente de la función. Si la pendiente es positiva en un intervalo, entonces la función es creciente en ese intervalo.
Comparación con tablas
Una forma útil de visualizar la información sobre en qué intervalo una función de la gráfica es creciente es a través del uso de tablas. Las tablas son una herramienta común para organizar y presentar información de una manera clara y fácil de entender.
Por ejemplo, podríamos crear una tabla HTML que muestre la función f(x) = x^2 y en qué intervalo es creciente:
| x | f(x) = x^2 |
|---|---|
| -∞ < x < 0 | Decreciente |
| x = 0 | Mínimo |
| 0 < x < ∞ | Creciente |
Como podemos ver en esta tabla, la función f(x) = x^2 es creciente en el intervalo [0, ∞), lo que coincide con lo que descubrimos anteriormente al examinar la gráfica de la función.
Preguntas frecuentes
¿Puede una función ser creciente y decreciente al mismo tiempo?
No, una función solo puede ser creciente o decreciente. Si una función cambia de dirección, entonces se considera que tiene un punto crítico donde la pendiente es cero.
¿Cómo se determina la pendiente de una función?
La pendiente de una función se puede determinar mediante el cálculo de la derivada de la función.
¿Qué significa que una función sea constante?
Una función constante es una función cuyo valor no cambia a medida que su entrada cambia. En otras palabras, si evaluamos una función constante en cualquier valor de x, obtendremos el mismo valor constante.
¿Qué es una función decreciente?
Una función decreciente es una función cuyo valor disminuye a medida que su entrada aumenta. En otras palabras, si aumentamos el valor de x en una función decreciente f(x), entonces el valor de f(x) disminuirá.
¿Cómo se grafica una función?
Para graficar una función, es útil primero construir una tabla de valores que muestre algunos puntos clave de la función. Luego, podemos usar estos puntos para trazar la curva de la función en un sistema de coordenadas.

Deja una respuesta