Figuras cuyas diagonales no se cruzan por su punto medio
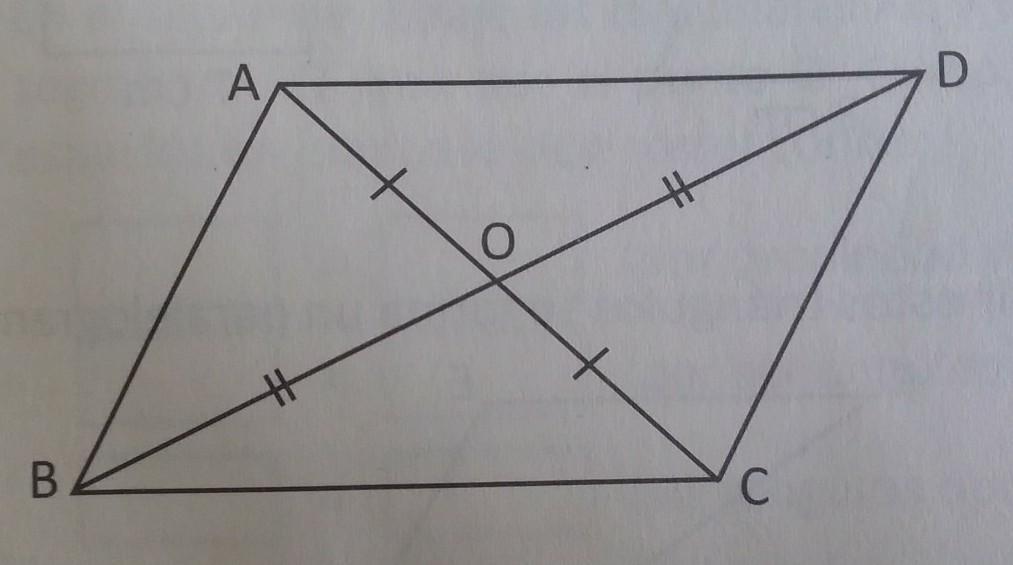
En la geometría, existen figuras que tienen diagonales que no se cruzan por su punto medio. Esto puede parecer contradictorio, ya que en la mayoría de las figuras geométricas, las diagonales se cruzan en el punto medio. Sin embargo, hay algunas excepciones interesantes que exploraremos en este artículo.
Las figuras que tienen diagonales que no se cruzan por su punto medio son aquellas que no tienen simetría axial. Es decir, no son iguales en ambos lados de una línea de simetría. Estas figuras son conocidas como asimétricas o irregulares.
Las figuras irregulares más comunes que tienen diagonales que no se cruzan por su punto medio son los trapecios y los rombos. En el caso del trapecio, las diagonales se cruzan en un punto que no es el punto medio. En el caso del rombo, las diagonales se cruzan en un ángulo recto, pero no en el punto medio.
Una forma de visualizar esto es a través de la tabla HTML a continuación:
| Figura | Diagonales |
|---|---|
| Trapecio | No se cruzan por el punto medio |
| Rombo | No se cruzan por el punto medio |
Ahora, profundicemos en cada figura y veamos cómo funcionan sus diagonales.
Trapecios
Un trapecio es una figura con cuatro lados, donde dos lados son paralelos entre sí y los otros dos no lo son. Las diagonales de un trapecio se cortan en un punto que no es el punto medio de la figura. Este punto de intersección se encuentra más cerca del lado más largo del trapecio.
Para visualizar esto, imagina un trapecio con los lados paralelos AB y CD, y las diagonales AC y BD. Si dibujas las diagonales en la figura, verás que se cruzan en un punto que está más cerca del lado CD que del lado AB.
Rombos
Un rombo es una figura con cuatro lados iguales y ángulos opuestos iguales. Las diagonales de un rombo se cortan en un ángulo recto, pero no en el punto medio de la figura.
Para visualizar esto, imagina un rombo con diagonales AC y BD. Si dibujas las diagonales en la figura, verás que se cruzan en un ángulo recto en el centro del rombo, pero no en el punto medio de cada diagonal.
Pentágonos y hexágonos irregulares
Además de los trapecios y los rombos, también existen pentágonos y hexágonos irregulares que tienen diagonales que no se cruzan por su punto medio. Estas figuras pueden ser más difíciles de visualizar, pero es posible demostrar matemáticamente que sus diagonales no se cruzan en el punto medio.
¿Por qué es importante conocer estas figuras?
Conocer estas figuras y cómo funcionan sus diagonales puede ser útil en varios campos, como la arquitectura y la ingeniería. Por ejemplo, en la construcción de puentes y edificios, es importante entender cómo las fuerzas se distribuyen a través de las diagonales de una estructura. Si las diagonales no se cruzan por el punto medio, esto puede afectar la resistencia y la estabilidad de la estructura.
¿Cuál es la diferencia entre un trapecio y un paralelogramo?
A menudo, se confunden los términos "trapecio" y "paralelogramo". Ambas figuras tienen lados paralelos, pero la diferencia es que un trapecio tiene solo dos lados paralelos, mientras que un paralelogramo tiene todos sus lados paralelos. Además, los ángulos opuestos de un paralelogramo son iguales, mientras que en un trapecio solo los ángulos opuestos de los lados paralelos son iguales.
¿Por qué algunas figuras tienen diagonales que se cruzan en el punto medio?
En la mayoría de las figuras geométricas, las diagonales se cruzan en el punto medio porque la figura tiene simetría axial. Esto significa que la figura es igual en ambos lados de una línea de simetría. En estas figuras, las diagonales se cruzan en el punto medio porque los puntos de la figura están equidistantes de la línea de simetría.
¿Existen figuras con más de dos diagonales?
Sí, hay figuras con más de dos diagonales. Por ejemplo, un hexágono tiene nueve diagonales. Además, hay figuras como el octógono, el decágono y el dodecágono que tienen muchas diagonales diferentes.
¿Por qué es importante entender la geometría?
Entender la geometría puede ser útil en muchos campos, desde la arquitectura y la ingeniería hasta la física y la informática. La geometría también puede ayudar a desarrollar habilidades de pensamiento crítico y resolución de problemas, ya que requiere visualización y razonamiento lógico. Además, la geometría puede ser una herramienta útil para mejorar la comprensión de otras áreas de las matemáticas, como el álgebra y el cálculo.

Deja una respuesta