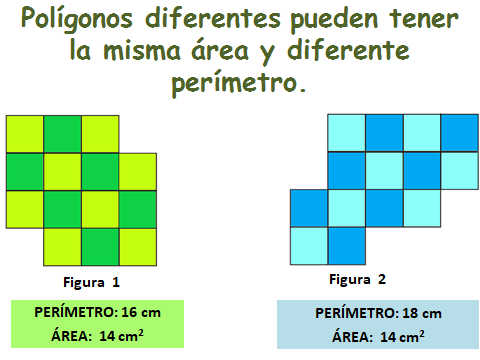
Figuras distintas que tengan la misma area pero diferente perimetro
Las figuras geométricas son una parte importante de las matemáticas y la geometría, y podemos encontrar una gran variedad de ellas. Algunas de estas figuras pueden tener la misma área pero un perímetro diferente. En este artículo, exploraremos algunas de estas figuras y cómo se relacionan entre sí.
¿Qué es el perímetro y el área?
Antes de adentrarnos en la comparación de figuras con diferentes perímetros y áreas, es importante entender qué significan estos términos.
El perímetro de una figura es la medida de la distancia alrededor de su borde. Es decir, la suma de las longitudes de todos sus lados. Por otro lado, el área de una figura es la cantidad de espacio que ocupa en una superficie plana. Se mide en unidades cuadradas y se calcula multiplicando la base por la altura de la figura.
Ejemplos de figuras con la misma área pero diferente perímetro
Rectángulo y cuadrado
Un rectángulo y un cuadrado pueden tener la misma área, pero el perímetro del cuadrado será mayor que el del rectángulo. Esto se debe a que el cuadrado tiene lados iguales, mientras que el rectángulo tiene lados de diferentes longitudes. Por ejemplo, un rectángulo de 4 unidades de ancho y 8 unidades de largo tiene un área de 32 unidades cuadradas y un perímetro de 24 unidades. En cambio, un cuadrado de 5.65 unidades de lado también tiene un área de 32 unidades cuadradas, pero su perímetro es de 22.6 unidades.
Círculo y rectángulo
Un círculo y un rectángulo también pueden tener la misma área, pero el perímetro del rectángulo será mayor que el del círculo. Esto se debe a que el círculo tiene una forma más redondeada y uniforme, mientras que el rectángulo tiene esquinas y bordes rectos. Por ejemplo, un rectángulo de 4 unidades de ancho y 8 unidades de largo tiene un área de 32 unidades cuadradas y un perímetro de 24 unidades. En cambio, un círculo de aproximadamente 6.37 unidades de diámetro también tiene un área de 32 unidades cuadradas, pero su perímetro es de aproximadamente 20 unidades.
Comparación de figuras con tablas
Para comparar estas figuras y sus medidas de manera más visual, podemos utilizar tablas. A continuación, se presenta una tabla que muestra la comparación entre un rectángulo y un cuadrado con la misma área:
| Rectángulo | Cuadrado | |
|---|---|---|
| Área | 32 unidades cuadradas | 32 unidades cuadradas |
| Perímetro | 24 unidades | 22.6 unidades |
Como podemos observar en la tabla, el cuadrado tiene un área y un perímetro igual, mientras que el rectángulo tiene un perímetro mayor a pesar de tener la misma área.
listas para comparar figuras con la misma área
Otra manera de comparar figuras con la misma área pero diferentes perímetros es a través de listas. A continuación, se presentan dos listas que comparan un rectángulo y un cuadrado con la misma área:
Rectángulo
- Área: 32 unidades cuadradas
- Perímetro: 24 unidades
Cuadrado
- Área: 32 unidades cuadradas
- Perímetro: 22.6 unidades
Conclusión
En conclusión, Las figuras geométricas pueden tener la misma área pero diferentes perímetros. Esto se debe a que la forma y la longitud de los lados de cada figura afectan la cantidad de espacio que ocupa y la medida de su borde. Es importante entender la diferencia entre el perímetro y el área para poder comparar y entender estas figuras.
Preguntas frecuentes
¿Por qué es importante entender la diferencia entre el perímetro y el área?
Es importante entender la diferencia entre el perímetro y el área para poder comparar y entender diferentes figuras geométricas. Esto nos permite calcular y medir correctamente su tamaño y forma, lo cual es útil en muchos campos, como la arquitectura, la ingeniería y la física.
¿Cómo se calcula el perímetro y el área de un círculo?
El perímetro de un círculo se calcula multiplicando su diámetro por pi (3.14). El área se calcula multiplicando el radio al cuadrado por pi.
¿Por qué un cuadrado tiene un perímetro mayor que un rectángulo con la misma área?
Un cuadrado tiene un perímetro mayor que un rectángulo con la misma área porque todos sus lados son iguales, mientras que el rectángulo tiene lados de diferentes longitudes.
¿Cómo se calcula el área de un triángulo?
El área de un triángulo se calcula multiplicando la base por la altura y dividiendo el resultado entre 2.

Deja una respuesta