Geometricamente que representa el limite de una suma de riemann

El cálculo integral es una de las ramas más importantes de las matemáticas. La suma de Riemann es una técnica fundamental en el cálculo integral. Es una manera de aproximarse a la integral de una función mediante la suma de áreas de rectángulos. El límite de una suma de Riemann es la representación geométrica de la integral de una función.

Antes de profundizar en el tema, es importante recordar que una integral es una herramienta matemática que nos permite calcular el área bajo una curva. La integral de una función nos da el valor de la acumulación de pequeñas áreas de la curva en un intervalo específico.

La suma de Riemann es una técnica para calcular una aproximación de la integral de una función. La idea es dividir el intervalo en pequeñas subintervalos, y luego aproximar la curva con rectángulos. Cada rectángulo tiene un ancho igual a la longitud del subintervalo, y una altura igual al valor de la función en el punto medio de ese subintervalo. La suma de Riemann es la suma de las áreas de todos los rectángulos.

Cuando se aumenta el número de subintervalos, se reduce el ancho de cada rectángulo, y por lo tanto, la aproximación se vuelve más precisa. El límite de la suma de Riemann es la representación geométrica de la integral de la función.

Geometricamente, el límite de una suma de Riemann representa el área exacta debajo de la curva de la función en el intervalo dado. A medida que se aumenta el número de subintervalos, la aproximación se vuelve más precisa y la suma de Riemann se acerca cada vez más al valor real de la integral.

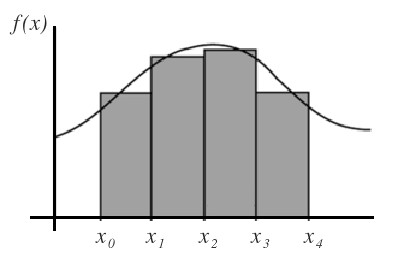
La figura a continuación muestra una representación geométrica de la suma de Riemann para la función f(x) = x^2 en el intervalo [0,2]:


En la figura, los rectángulos de color rojo representan la aproximación de la curva de la función f(x) mediante la suma de Riemann. Como se puede observar, a medida que se aumenta el número de subintervalos, la aproximación se vuelve más precisa y los rectángulos se acercan cada vez más a la curva real de la función.

En conclusión, El límite de una suma de Riemann representa la integral de una función en un intervalo específico. Geométricamente, se puede visualizar como el área debajo de la curva de la función en ese intervalo. La suma de Riemann es una técnica fundamental en el cálculo integral y es esencial para comprender el concepto de límite y la aproximación de funciones.

Preguntas frecuentes:

1. ¿Cómo se calcula una suma de Riemann?
Para calcular una suma de Riemann, se divide el intervalo en subintervalos, se aproxima la curva con rectángulos y se suma el área de todos los rectángulos.

2. ¿Cómo se representa geométricamente el límite de una suma de Riemann?
El límite de una suma de Riemann se representa geométricamente como el área debajo de la curva de la función en el intervalo dado.

3. ¿Por qué es importante la suma de Riemann en el cálculo integral?
La suma de Riemann es una técnica fundamental en el cálculo integral porque nos permite aproximar el valor de la integral de una función.

4. ¿Cómo se puede mejorar la precisión de la aproximación de la suma de Riemann?
La precisión de la aproximación de la suma de Riemann se puede mejorar aumentando el número de subintervalos.

5. ¿Se puede aplicar la suma de Riemann a cualquier función?
Sí, la suma de Riemann se puede aplicar a cualquier función siempre y cuando sea integrable en el intervalo dado.