Hallar dw dt utilizando la regla de la cadena apropiada

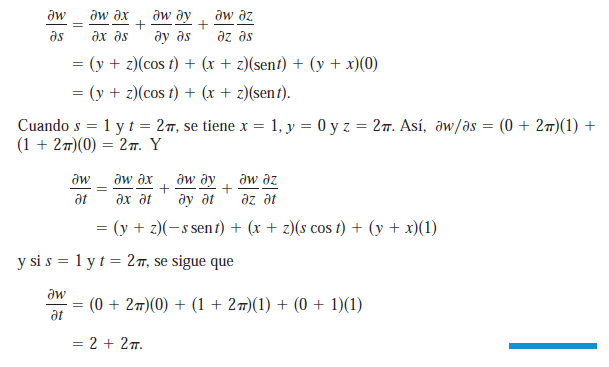
Cuando se trabaja con cálculo diferencial, es común encontrarse con problemas que involucren la tasa instantánea de cambio de una función. En particular, cuando se trabaja con funciones compuestas, es necesario utilizar la regla de la cadena para hallar la tasa de cambio de la función compuesta en un punto específico. En este artículo, te explicaremos cómo utilizar la regla de la cadena apropiada para hallar dw dt.

¿Qué es la regla de la cadena?

La regla de la cadena es una herramienta fundamental en cálculo diferencial que nos permite calcular la derivada de una función compuesta. En su forma más básica, la regla de la cadena establece que si f(x) y g(x) son dos funciones diferenciables, entonces la derivada de la función compuesta h(x) = f(g(x)) se puede calcular como:

(h(x))' = f'(g(x)) * g'(x)

Es decir, la derivada de la función compuesta es igual a la derivada de la función exterior evaluada en la función interior multiplicada por la derivada de la función interior.

Aplicando la regla de la cadena apropiada

Para hallar dw dt utilizando la regla de la cadena apropiada, es necesario tener en cuenta que la variable t es la variable independiente y que w es una función compuesta de t. Es decir, w(t) = f(g(t)), donde f y g son funciones diferenciables.

Si queremos hallar la tasa instantánea de cambio de w con respecto al tiempo, es decir, dw dt, entonces podemos aplicar la regla de la cadena de la siguiente manera:

(dw dt) = (df dg) * (dg dt)

Donde df dg es la derivada de la función exterior f evaluada en la función interior g, y dg dt es la derivada de la función interior g con respecto al tiempo.

Ejemplo

Supongamos que tenemos la siguiente función compuesta:

w(t) = cos(2t^2 + 3t)

Para hallar dw dt utilizando la regla de la cadena apropiada, podemos identificar que la función exterior es la función coseno y la función interior es 2t^2 + 3t. Entonces, podemos aplicar la regla de la cadena de la siguiente manera:

(dw dt) = (-sen(2t^2 + 3t)) * (4t + 3)

Es decir, la tasa instantánea de cambio de w con respecto al tiempo es igual a la derivada de la función exterior evaluada en la función interior multiplicada por la derivada de la función interior.

Comparación con tablas

Así como la regla de la cadena es una herramienta fundamental en cálculo diferencial, las tablas son una herramienta fundamental en el desarrollo web. Las tablas nos permiten organizar la información en filas y columnas, y son muy útiles para mostrar datos numéricos o comparar información.

Al igual que en la regla de la cadena, en las tablas es importante identificar cuál es la información que se quiere mostrar y cómo se relaciona esa información. En el caso de la regla de la cadena, es importante identificar cuál es la función exterior y cuál es la función interior para poder aplicar correctamente la regla. En el caso de las tablas, es importante identificar cuáles son los datos que se quieren mostrar y cómo se relacionan entre sí para poder organizar correctamente la información.

Preguntas frecuentes

¿Por qué es importante utilizar la regla de la cadena?

Es importante utilizar la regla de la cadena porque nos permite calcular la derivada de funciones compuestas, que son muy comunes en cálculo diferencial. Además, muchas aplicaciones de las matemáticas en la ciencia y la ingeniería involucran funciones compuestas, por lo que la regla de la cadena es una herramienta fundamental para resolver problemas prácticos.

¿Cómo sé cuál es la función exterior y cuál es la función interior?

En la mayoría de los casos, la función exterior es la función que se aplica al resultado de la función interior. Por ejemplo, si tenemos la función w(t) = cos(2t^2 + 3t), la función exterior es la función coseno y la función interior es 2t^2 + 3t. Sin embargo, en algunos casos puede ser más difícil identificar cuál es la función exterior y cuál es la función interior, por lo que es importante practicar y familiarizarse con la regla de la cadena para poder aplicarla correctamente.

¿Cómo puedo verificar si mi respuesta es correcta?

Para verificar si tu respuesta es correcta, puedes utilizar la definición de la derivada y calcular la tasa de cambio de la función compuesta utilizando límites. También puedes utilizar herramientas como Wolfram Alpha o la calculadora de derivadas en línea para verificar tu respuesta.

¿La regla de la cadena solo se aplica a funciones compuestas?

Sí, la regla de la cadena solo se aplica a funciones compuestas. Para hallar la derivada de una función no compuesta, es necesario utilizar otras herramientas del cálculo diferencial, como la regla de la potencia o la regla del producto.

¿La regla de la cadena se puede utilizar para calcular la segunda derivada?

Sí, la regla de la cadena se puede utilizar para calcular la segunda derivada de una función compuesta. Para calcular la segunda derivada, es necesario aplicar la regla de la cadena dos veces, utilizando la derivada de la primera derivada como función exterior y la segunda derivada como función interior.