Intervalo de confianza para la media de una distribucion normal

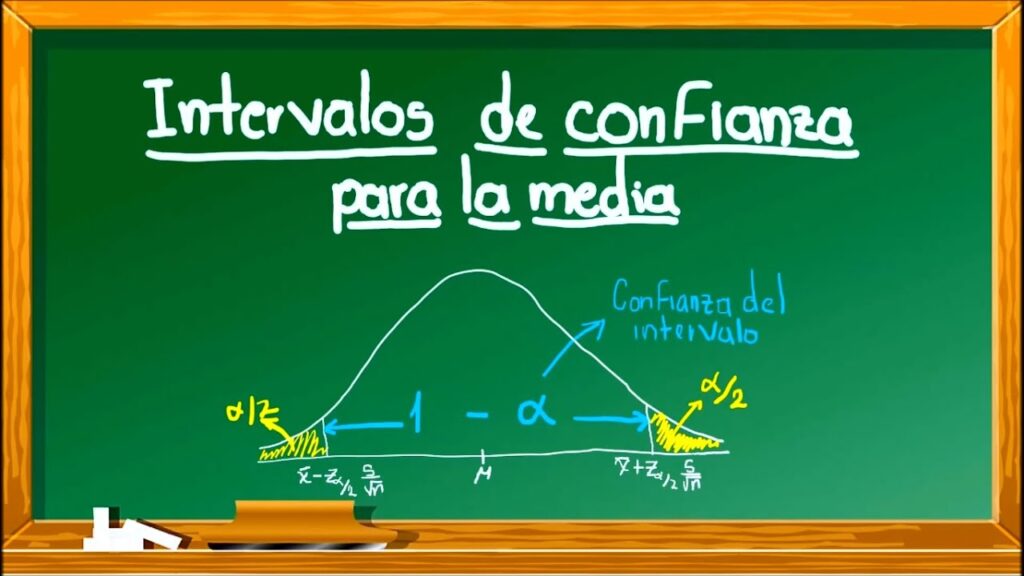
Cuando se trabaja con datos estadísticos, es común que se quiera estimar el valor real de una población a partir de una muestra. En este caso, el intervalo de confianza para la media de una distribución normal es una herramienta que permite determinar un rango de valores probables para la media poblacional.

¿Qué es un intervalo de confianza?

Un intervalo de confianza es un rango de valores que se obtiene a partir de una muestra y que se utiliza para estimar un valor desconocido de la población. En este caso, el intervalo de confianza para la media de una distribución normal es un rango de valores que contiene la estimación más probable de la media poblacional.

¿Cómo se calcula el intervalo de confianza?

El intervalo de confianza se calcula a partir de la muestra y de un nivel de confianza determinado. El nivel de confianza es una medida de la probabilidad de que el valor real de la población se encuentre dentro del intervalo de confianza. Por ejemplo, si el nivel de confianza es del 95%, existe una probabilidad del 95% de que el valor real de la población se encuentre dentro del intervalo de confianza.

Para calcular el intervalo de confianza para la media de una distribución normal, se utiliza la fórmula:

Intervalo de confianza = X̄ ± Zα/2 * (σ / √n)

Donde:

- X̄ es la media muestral
- Zα/2 es el valor crítico de la distribución normal estándar que corresponde al nivel de confianza deseado. Este valor se encuentra en la tabla Z o se puede calcular utilizando una calculadora de distribución normal.
- σ es la desviación estándar poblacional (en caso de que se conozca) o la desviación estándar muestral (en caso de que no se conozca).
- n es el tamaño de la muestra.

¿Qué significa el valor de Zα/2?

El valor de Zα/2 es el valor crítico de la distribución normal estándar que corresponde al nivel de confianza deseado. Este valor se encuentra en la tabla Z o se puede calcular utilizando una calculadora de distribución normal.

Por ejemplo, si se desea calcular un intervalo de confianza con un nivel de confianza del 95%, el valor de Zα/2 es 1.96. Esto significa que el 95% de las veces que se calcula un intervalo de confianza con un nivel de confianza del 95%, el valor real de la población estará dentro del intervalo de confianza.

¿Cómo se interpreta el intervalo de confianza?

El intervalo de confianza se interpreta como un rango de valores que contiene la estimación más probable de la media poblacional. Por ejemplo, si se obtiene un intervalo de confianza de 20 a 30 para la media poblacional de una variable, esto significa que existe una probabilidad del 95% de que el valor real de la media poblacional esté dentro de ese rango.

Comparación con tablas y listas

Para ilustrar la comparación entre el intervalo de confianza y las tablas y listas, se puede utilizar el siguiente ejemplo:

Supongamos que se quiere estimar la altura promedio de los estudiantes de una universidad. Se toma una muestra de 100 estudiantes y se obtiene una media muestral de 170 cm y una desviación estándar muestral de 5 cm. Se desea calcular un intervalo de confianza del 95% para la media poblacional.

Utilizando la fórmula anterior, se obtiene un intervalo de confianza de 168.4 a 171.6 cm. Esto significa que existe una probabilidad del 95% de que la altura promedio de todos los estudiantes de la universidad se encuentre dentro de ese rango.

En comparación, una tabla HTML podría mostrar la cantidad de estudiantes por altura, mientras que una lista HTML podría mostrar la altura de cada estudiante de la muestra.

Conclusion

El intervalo de confianza para la media de una distribución normal es una herramienta estadística importante que permite estimar el valor real de una población a partir de una muestra. Para calcular el intervalo de confianza, se utiliza la fórmula que depende del tamaño de la muestra, la media muestral, la desviación estándar poblacional o muestral, y el nivel de confianza deseado.

Preguntas frecuentes

1. ¿Qué es un nivel de confianza?
El nivel de confianza es una medida de la probabilidad de que el valor real de la población se encuentre dentro del intervalo de confianza. Por ejemplo, si el nivel de confianza es del 95%, existe una probabilidad del 95% de que el valor real de la población se encuentre dentro del intervalo de confianza.

2. ¿Qué es la distribución normal?
La distribución normal es una distribución de probabilidad continua que se utiliza para modelar muchos fenómenos naturales y sociales. Es conocida también como la campana de Gauss debido a su forma característica.

3. ¿Cómo se obtiene el valor crítico de la distribución normal estándar?
El valor crítico de la distribución normal estándar se puede obtener utilizando una tabla Z o una calculadora de distribución normal. Este valor depende del nivel de confianza deseado y se utiliza para calcular el intervalo de confianza.

4. ¿Qué es la desviación estándar?
La desviación estándar es una medida de dispersión que indica cuánto se alejan los datos de la media. Es una medida de la variabilidad de los datos.

5. ¿Cómo se interpreta el intervalo de confianza?
El intervalo de confianza se interpreta como un rango de valores que contiene la estimación más probable de la media poblacional. Por ejemplo, si se obtiene un intervalo de confianza de 20 a 30 para la media poblacional de una variable, esto significa que existe una probabilidad del 95% de que el valor real de la media poblacional esté dentro de ese rango.