Linea del tiempo de la geometria analitica hasta la actualidad

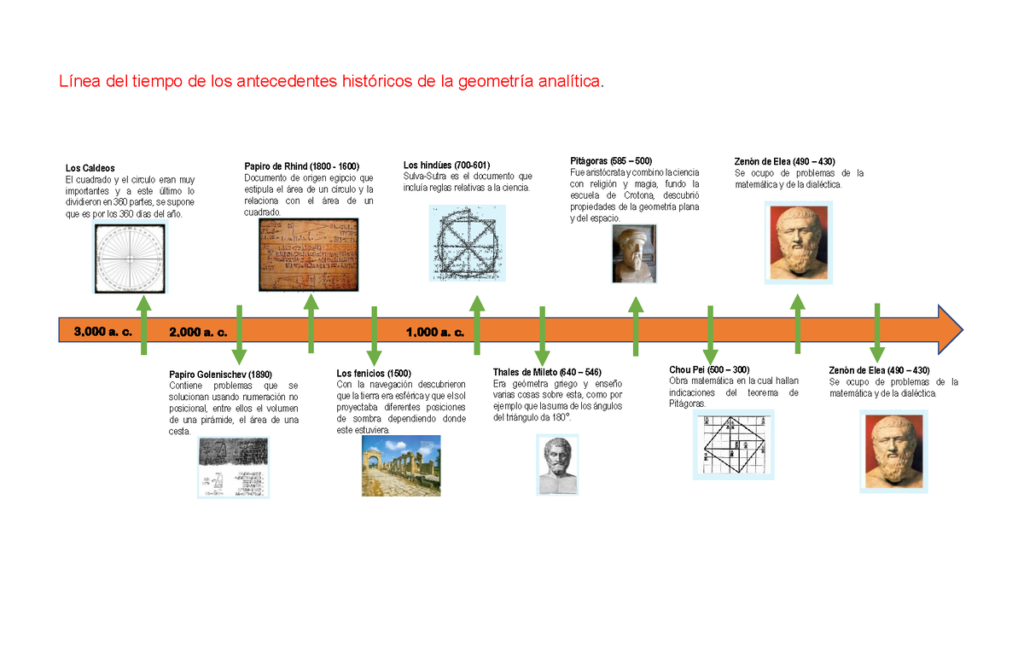
La geometría analítica es una rama de las matemáticas que combina elementos de la geometría y el álgebra para resolver problemas geométricos. La historia de la geometría analítica se remonta a la antigua Grecia, cuando Euclides y Apolonio trabajaron en problemas geométricos utilizando la geometría pura. Sin embargo, no fue hasta el siglo XVII que se desarrolló la geometría analítica como la conocemos hoy en día, gracias a los trabajos de René Descartes y Pierre de Fermat. A continuación, presentamos una línea del tiempo de la geometría analítica hasta la actualidad.

Siglo XVII

En 1637, René Descartes publicó su obra "La Geometría", donde introdujo el concepto de coordenadas cartesianas y la idea de que las figuras geométricas podían ser representadas por ecuaciones algebraicas. Esto permitió a los matemáticos trabajar con problemas geométricos utilizando técnicas algebraicas.

Siglo XVIII

En 1748, Leonhard Euler publicó "Introductio in analysin infinitorum", donde desarrolló el cálculo diferencial e integral utilizando la geometría analítica. Esto permitió a los matemáticos trabajar con problemas que involucraban curvas y superficies más complejas.

Siglo XIX

En 1819, Augustin-Louis Cauchy y Jean-Baptiste Joseph Fourier desarrollaron la teoría de las funciones analíticas, que permitió trabajar con funciones complejas y las transformadas de Fourier. También en este siglo, Nikolai Lobachevsky y János Bolyai desarrollaron la geometría no euclidiana, que estudió figuras geométricas en un espacio curvo.

Siglo XX

En 1901, David Hilbert propuso los 23 problemas de Hilbert, uno de los cuales pedía una axiomatización completa de la geometría analítica. En 1931, Kurt Gödel demostró que esto era imposible utilizando el teorema de incompletitud de Gödel. En 1954, André Weil y Oscar Zariski desarrollaron la teoría de variedades algebraicas, que permitió trabajar con soluciones algebraicas de ecuaciones polinómicas.

Actualidad

En la actualidad, la geometría analítica sigue siendo una herramienta importante en la investigación matemática y en aplicaciones prácticas en ingeniería y ciencias de la computación. Los avances en la computación y la visualización de datos han permitido trabajar con figuras geométricas de mayor complejidad y en más dimensiones. Además, se han desarrollado nuevas ramas de la geometría como la geometría discreta y la geometría computacional.

En resumen, La geometría analítica ha evolucionado significativamente a lo largo de los siglos, desde la introducción de las coordenadas cartesianas hasta el desarrollo de la geometría no euclidiana y la teoría de variedades algebraicas. Actualmente, sigue siendo una herramienta importante en la investigación matemática y en aplicaciones prácticas en ingeniería y ciencias de la computación.

Preguntas frecuentes

¿Qué es la geometría analítica?

La geometría analítica es una rama de las matemáticas que combina elementos de la geometría y el álgebra para resolver problemas geométricos.

¿Quiénes fueron los principales contribuyentes al desarrollo de la geometría analítica?

René Descartes y Pierre de Fermat fueron los principales contribuyentes al desarrollo de la geometría analítica en el siglo XVII.

¿Qué es la geometría no euclidiana?

La geometría no euclidiana es una rama de la geometría que estudia figuras geométricas en un espacio curvo, en contraposición a la geometría euclidiana, que estudia figuras geométricas en un espacio plano.

¿Qué son las variedades algebraicas?

Las variedades algebraicas son objetos geométricos que se pueden definir mediante ecuaciones polinómicas. Esta teoría fue desarrollada por André Weil y Oscar Zariski en el siglo XX.

¿Cómo se utiliza la geometría analítica en la actualidad?

La geometría analítica sigue siendo una herramienta importante en la investigación matemática y en aplicaciones prácticas en ingeniería y ciencias de la computación, como en el diseño de circuitos electrónicos y en la visualización de datos.