Menciona algun metodo para resolver un sistema de ecuaciones lineales

Cuando nos enfrentamos a un sistema de ecuaciones lineales, es normal sentirnos abrumados por la cantidad de variables y ecuaciones que debemos resolver. Sin embargo, existen diferentes métodos que nos pueden ayudar a encontrar la solución de manera más sencilla y eficiente. Aquí te presento algunos de ellos:

1. Método de sustitución

Este método consiste en despejar una variable en una de las ecuaciones y sustituirla en la otra, de manera que se reduzca el número de incógnitas. Por ejemplo, si tenemos el siguiente sistema:

x + y = 5
2x - y = 1

Podemos despejar y en la primera ecuación:

y = 5 - x

Y sustituirla en la segunda ecuación:

2x - (5 - x) = 1

Resolviendo esta ecuación, obtenemos el valor de x:

x = 2

Luego, podemos sustituir este valor en la primera ecuación para encontrar el valor de y:

2 + y = 5
y = 3

Por lo tanto, la solución del sistema es x = 2, y = 3.

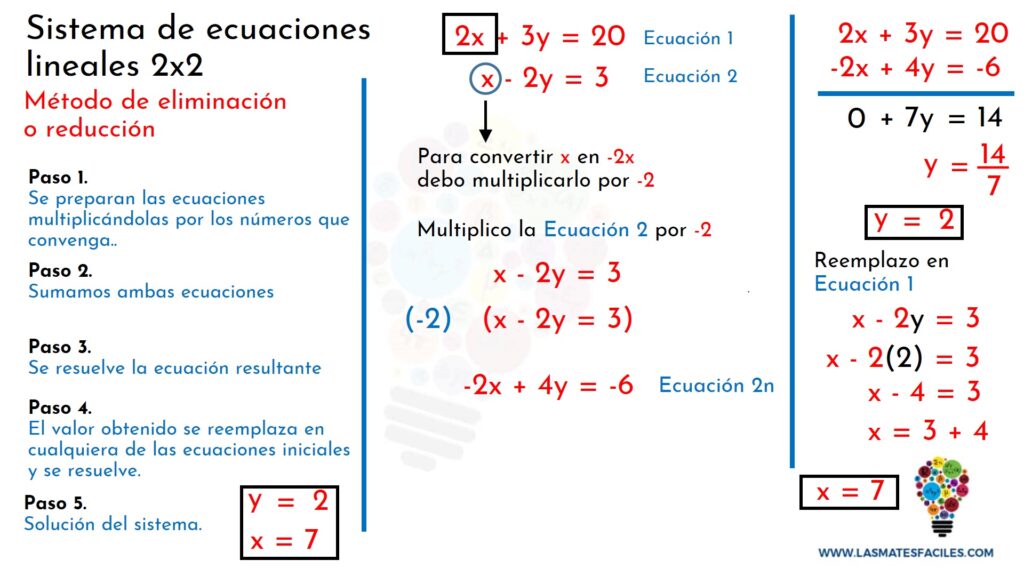
2. Método de eliminación

Este método consiste en sumar o restar las ecuaciones del sistema de manera que se elimine una de las variables. Por ejemplo, si tenemos el siguiente sistema:

2x + 3y = 7
4x - y = 1

Podemos multiplicar la segunda ecuación por 3 para que el coeficiente de y sea el mismo que en la primera ecuación:

2x + 3y = 7
12x - 3y = 3

Luego, podemos sumar las dos ecuaciones para eliminar la variable y:

14x = 10

Y, finalmente, despejar x:

x = 5/7

Sustituyendo este valor en una de las ecuaciones, podemos encontrar el valor de y:

2(5/7) + 3y = 7
y = 13/21

Por lo tanto, la solución del sistema es x = 5/7, y = 13/21.

3. Método de Gauss-Jordan

Este método consiste en transformar el sistema en una matriz aumentada y aplicar operaciones elementales de fila para obtener una matriz escalonada reducida. Por ejemplo, si tenemos el siguiente sistema:

2x + y - z = 5
x - y + z = 2
3x + 2y - z = 8

Podemos escribirlo como una matriz aumentada:

[2 1 -1 | 5]
[1 -1 1 | 2]
[3 2 -1 | 8]

Luego, aplicamos operaciones elementales de fila para obtener una matriz escalonada reducida:

[1 0 0 | 1]
[0 1 0 | 2]
[0 0 1 | 3]

La última fila nos indica que z = 3. Sustituyendo este valor en la segunda fila, obtenemos que y = 2. Finalmente, sustituyendo los valores de y y z en la primera fila, encontramos que x = 1. Por lo tanto, la solución del sistema es x = 1, y = 2, z = 3.

4. Método de Cramer

Este método utiliza determinantes para encontrar la solución del sistema. Para aplicarlo, debemos escribir el sistema en forma matricial:

[A][X] = [B]

Donde [A] es la matriz de coeficientes, [X] es la matriz de variables y [B] es la matriz de términos independientes. Luego, calculamos el determinante de [A] y los determinantes de las matrices [A] con una columna reemplazada por [B] en cada caso. La solución del sistema es el cociente entre cada uno de estos determinantes y el determinante de [A]. Por ejemplo, si tenemos el siguiente sistema:

2x + y - z = 5
x - y + z = 2
3x + 2y - z = 8

Podemos escribirlo en forma matricial:

[2 1 -1][x] [5]
[1 -1 1][y] = [2]
[3 2 -1][z] [8]

Calculando los determinantes, obtenemos:

|2 1 -1| |5 1 -1| |2 1 5|
|1 -1 1| = |-1 2 1| = |-1 2 1|
|3 2 -1| |8 2 1 | |3 2 8|

Y la solución del sistema es:

x = |2 1 5| / |2 1 -1| = 1
y = |-1 2 1| / |2 1 -1| = 2
z = |3 2 8| / |2 1 -1| = 3

Conclusión

Resolver un sistema de ecuaciones lineales puede parecer complicado al principio, pero existen diferentes métodos que nos pueden ayudar a encontrar la solución de manera más sencilla y eficiente. El método de sustitución, el método de eliminación, el método de Gauss-Jordan y el método de Cramer son solo algunos ejemplos de los métodos que podemos utilizar para resolver sistemas de ecuaciones lineales.

Preguntas frecuentes

1. ¿Qué es un sistema de ecuaciones lineales?

Un sistema de ecuaciones lineales es un conjunto de dos o más ecuaciones lineales con varias variables que deben ser resueltas simultáneamente.

2. ¿Qué es el método de sustitución?

El método de sustitución consiste en despejar una variable en una de las ecuaciones y sustituirla en la otra, de manera que se reduzca el número de incógnitas.

3. ¿Qué es el método de eliminación?

El método de eliminación consiste en sumar o restar las ecuaciones del sistema de manera que se elimine una de las variables.

4. ¿Qué es el método de Gauss-Jordan?

El método de Gauss-Jordan consiste en transformar el sistema en una matriz aumentada y aplicar operaciones elementales de fila para obtener una matriz escalonada reducida.

5. ¿Qué es el método de Cramer?

El método de Cramer utiliza determinantes para encontrar la solución del sistema.