Metodos de solucion de un sistema de ecuaciones lineales 2x2
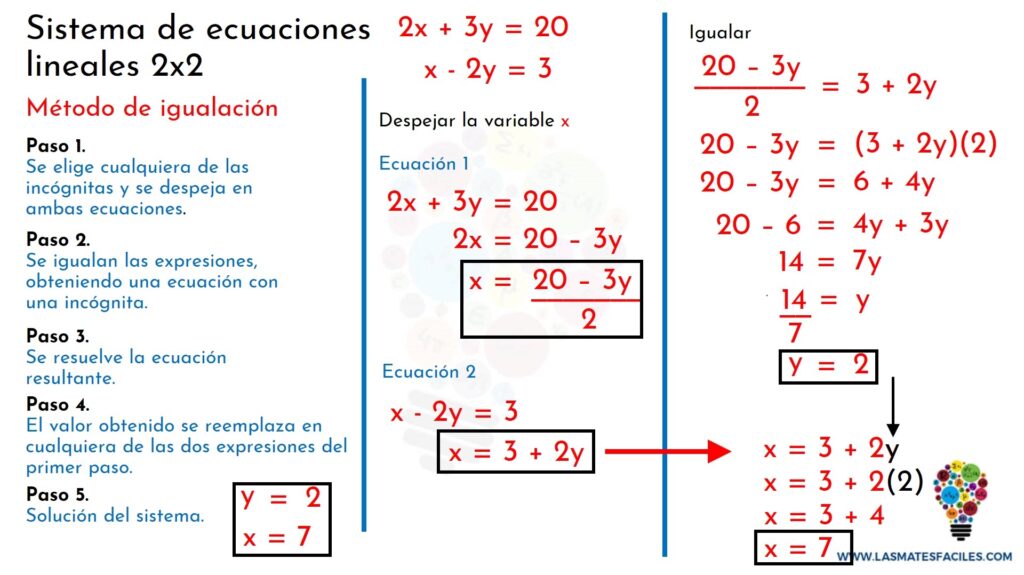
Cuando nos encontramos con un sistema de ecuaciones lineales 2x2, existen varias formas de encontrar su solución. En este artículo, vamos a explorar los métodos más comunes para resolver este tipo de problemas.
- Método de sustitución
- Método de eliminación
- Método de determinantes
- Tabla comparativa
- Preguntas frecuentes
- ¿Por qué es importante saber resolver sistemas de ecuaciones lineales 2x2?
- ¿Cuál es el método más rápido para resolver un sistema de ecuaciones lineales 2x2?
- ¿Puedo usar una calculadora para resolver sistemas de ecuaciones lineales 2x2?
- ¿Qué pasa si un sistema de ecuaciones lineales 2x2 no tiene solución?
- ¿Qué pasa si un sistema de ecuaciones lineales 2x2 tiene infinitas soluciones?
Método de sustitución
El método de sustitución es uno de los métodos más sencillos para resolver un sistema de ecuaciones lineales 2x2. En este método, se despeja una de las variables en una de las ecuaciones y se sustituye en la otra ecuación, obteniendo una ecuación con una sola variable. Luego, se resuelve esta ecuación y se encuentra el valor de una de las variables. Finalmente, se sustituye este valor en cualquiera de las dos ecuaciones originales para encontrar el valor de la otra variable.
Por ejemplo, si tenemos el siguiente sistema de ecuaciones:
x + y = 5
2x - y = 3
Podemos despejar y en la primera ecuación y obtener:
y = 5 - x
Luego, sustituimos esta expresión en la segunda ecuación y obtenemos:
2x - (5 - x) = 3
Resolviendo esta ecuación, encontramos que x = 2. Sustituyendo este valor en la primera ecuación, encontramos que y = 3.
Método de eliminación
El método de eliminación es otro método común para resolver un sistema de ecuaciones lineales 2x2. En este método, se eliminan una de las variables de las dos ecuaciones sumándolas o restándolas. Para ello, se multiplican ambas ecuaciones por un número adecuado de tal forma que los coeficientes de una de las variables sean iguales en ambas ecuaciones. Luego, se suman o restan las ecuaciones para eliminar una de las variables. Finalmente, se resuelve la ecuación resultante para encontrar el valor de una de las variables. Luego, se sustituye este valor en cualquiera de las dos ecuaciones originales para encontrar el valor de la otra variable.
Por ejemplo, si tenemos el siguiente sistema de ecuaciones:
2x + y = 5
4x - 2y = 6
Podemos multiplicar la primera ecuación por -2 para obtener:
-4x - 2y = -10
Luego, sumamos esta ecuación con la segunda ecuación para obtener:
-4x - 2y + 4x - 2y = -10 + 6
Simplificando, obtenemos:
-4y = -4
Resolviendo esta ecuación, encontramos que y = 1. Sustituyendo este valor en la primera ecuación, encontramos que x = 2.
Método de determinantes
El método de determinantes es otro método para resolver un sistema de ecuaciones lineales 2x2. En este método, se utiliza la matriz de coeficientes del sistema de ecuaciones para encontrar el valor de las variables. Para ello, se calcula el determinante de la matriz de coeficientes y se calcula el determinante de la matriz obtenida al sustituir la columna de términos independientes por los valores constantes del sistema de ecuaciones. Finalmente, se divide el determinante de la matriz de términos independientes por el determinante de la matriz de coeficientes para encontrar el valor de una de las variables. Luego, se sustituye este valor en cualquiera de las dos ecuaciones originales para encontrar el valor de la otra variable.
Por ejemplo, si tenemos el siguiente sistema de ecuaciones:
x + y = 5
2x - y = 3
Podemos escribir la matriz de coeficientes del sistema de ecuaciones como:
| 1 1 |
| 2 -1 |
La matriz de términos independientes es:
| 5 |
| 3 |
El determinante de la matriz de coeficientes es:
1*(-1) - 2*1 = -3
La matriz obtenida al sustituir la columna de términos independientes por los valores constantes del sistema de ecuaciones es:
| 5 1 |
| 3 -1 |
El determinante de esta matriz es:
5*(-1) - 3*1 = -8
Dividiendo el determinante de la matriz de términos independientes por el determinante de la matriz de coeficientes, encontramos que x = 2. Sustituyendo este valor en la primera ecuación, encontramos que y = 3.
Tabla comparativa
A continuación, presentamos una tabla comparativa de los métodos de solución de un sistema de ecuaciones lineales 2x2:
| Método | Ventajas | Desventajas |
|---|---|---|
| Sustitución | Fácil de entender y aplicar. | Puede ser tedioso y requiere de muchas operaciones. |
| Eliminación | Más rápido que el método de sustitución. | Requiere encontrar el número adecuado para multiplicar las ecuaciones. |
| Determinantes | Funciona para cualquier sistema de ecuaciones lineales. | Requiere calcular determinantes, lo cual puede ser complicado. |
Preguntas frecuentes
¿Por qué es importante saber resolver sistemas de ecuaciones lineales 2x2?
Los sistemas de ecuaciones lineales 2x2 son muy comunes en muchos campos, como la física, la ingeniería y la economía. Saber resolver estos sistemas es esencial para poder modelar y resolver problemas en estos campos.
¿Cuál es el método más rápido para resolver un sistema de ecuaciones lineales 2x2?
El método más rápido depende del sistema de ecuaciones en cuestión y de la habilidad del solver. En general, el método de eliminación es más rápido que el método de sustitución, pero el método de determinantes puede ser más rápido en algunos casos.
¿Puedo usar una calculadora para resolver sistemas de ecuaciones lineales 2x2?
Sí, muchas calculadoras tienen una función para resolver sistemas de ecuaciones lineales 2x2. Sin embargo, es importante entender los métodos detrás de la solución para poder verificar la respuesta y entender el problema.
¿Qué pasa si un sistema de ecuaciones lineales 2x2 no tiene solución?
Si un sistema de ecuaciones lineales 2x2 no tiene solución, esto significa que las dos ecuaciones son inconsistentes y no se cortan en ningún punto. Esto puede ocurrir si las dos ecuaciones representan líneas paralelas en el plano.
¿Qué pasa si un sistema de ecuaciones lineales 2x2 tiene infinitas soluciones?
Si un sistema de ecuaciones lineales 2x2 tiene infinitas soluciones, esto significa que las dos ecuaciones representan la misma línea en el plano. En este caso, cualquier par de valores que satisfagan una de las ecuaciones

Deja una respuesta