Metodos para resolver ecuaciones de primer grado con dos incognitas

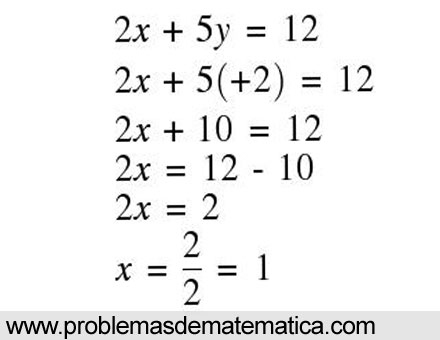
Las ecuaciones de primer grado con dos incognitas son aquellas que se presentan en la forma "ax + by = c", donde "a", "b" y "c" son números reales y "x" e "y" son las incógnitas. Resolver estas ecuaciones puede parecer complicado al principio, pero existen varios métodos que permiten encontrar la solución de manera sencilla y efectiva.

En este artículo, te explicaremos los métodos más comunes para resolver ecuaciones de primer grado con dos incógnitas, así como algunos ejemplos prácticos para que puedas aplicarlos en tus propios problemas matemáticos.

Método de sustitución

El método de sustitución es uno de los métodos más utilizados para resolver ecuaciones de primer grado con dos incógnitas. Consiste en despejar una de las variables en una de las ecuaciones y sustituirla en la otra ecuación. De esta manera, obtendremos una ecuación con una sola incógnita, que podremos resolver fácilmente.

Veamos un ejemplo para entenderlo mejor:

5x + 2y = 13

3x - y = 5

En este caso, podemos despejar "y" en la segunda ecuación:

y = 3x - 5

Ahora, sustituimos "y" en la primera ecuación:

5x + 2(3x - 5) = 13

Resolvemos la ecuación y obtenemos el valor de "x":

11x = 23

x = 2

Para encontrar el valor de "y", sustituimos "x" en cualquiera de las dos ecuaciones originales. En este caso, usaremos la segunda ecuación:

3(2) - y = 5

Resolvemos la ecuación y obtenemos el valor de "y":

y = 1

Por lo tanto, la solución de este sistema de ecuaciones es "x = 2" e "y = 1".

Método de igualación

El método de igualación consiste en despejar una de las variables en ambas ecuaciones y igualarlas. De esta manera, obtendremos una ecuación con una sola incógnita, que podremos resolver fácilmente.

Veamos un ejemplo para entenderlo mejor:

2x + 3y = 5

x - y = 1

En este caso, podemos despejar "x" en la segunda ecuación:

x = y + 1

Ahora, sustituimos "x" en la primera ecuación:

2(y + 1) + 3y = 5

Resolvemos la ecuación y obtenemos el valor de "y":

y = -1

Para encontrar el valor de "x", sustituimos "y" en cualquiera de las dos ecuaciones originales. En este caso, usaremos la segunda ecuación:

x - (-1) = 1

Resolvemos la ecuación y obtenemos el valor de "x":

x = 2

Por lo tanto, la solución de este sistema de ecuaciones es "x = 2" e "y = -1".

Método de eliminación

El método de eliminación consiste en sumar o restar las dos ecuaciones de manera que una de las variables se elimine. De esta manera, obtendremos una ecuación con una sola incógnita, que podremos resolver fácilmente.

Veamos un ejemplo para entenderlo mejor:

2x + 3y = 7

-2x + y = 1

En este caso, podemos multiplicar la segunda ecuación por "3" para obtener un coeficiente de "3y":

2x + 3y = 7

-6x + 3y = 3

Ahora, sumamos las dos ecuaciones:

-4x = 10

Resolvemos la ecuación y obtenemos el valor de "x":

x = -2.5

Para encontrar el valor de "y", sustituimos "x" en cualquiera de las dos ecuaciones originales. En este caso, usaremos la segunda ecuación:

-2(-2.5) + y = 1

Resolvemos la ecuación y obtenemos el valor de "y":

y = 6

Por lo tanto, la solución de este sistema de ecuaciones es "x = -2.5" e "y = 6".

Comparación con las tablas

Así como las tablas permiten organizar y presentar información de manera clara y ordenada, los métodos para resolver ecuaciones de primer grado con dos incógnitas nos permiten organizar y resolver problemas matemáticos de manera sencilla y eficiente. Ambos son herramientas valiosas que nos permiten presentar y entender la información de manera más efectiva.

listas

A continuación, presentamos una lista de los métodos para resolver ecuaciones de primer grado con dos incógnitas:

• Método de sustitución
• Método de igualación
• Método de eliminación

Conclusión

Las ecuaciones de primer grado con dos incógnitas son fundamentales en la matemática y su resolución es esencial en muchos campos, desde la física hasta la economía. Los métodos de sustitución, igualación y eliminación son herramientas valiosas que nos permiten resolver estos problemas de manera sencilla y eficiente. Con la práctica y el estudio, podremos dominar estos métodos y aplicarlos en nuestros propios problemas matemáticos.

Preguntas frecuentes

¿Qué son las ecuaciones de primer grado con dos incógnitas?

Son aquellas ecuaciones que se presentan en la forma "ax + by = c", donde "a", "b" y "c" son números reales y "x" e "y" son las incógnitas.

¿Por qué es importante resolver ecuaciones de primer grado con dos incógnitas?

La resolución de estas ecuaciones es esencial en muchos campos, desde la física hasta la economía. Además, nos permite desarrollar habilidades matemáticas que son fundamentales en nuestra vida diaria.

¿Cuáles son los métodos más comunes para resolver ecuaciones de primer grado con dos incógnitas?

Los métodos más comunes son el de sustitución, igualación y eliminación.

¿Qué es el método de sustitución?

Consiste en despejar una de las variables en una de las ecuaciones y sustituirla en la otra ecuación.

¿Qué es el método de igualación?

Consiste en despejar una de las variables en ambas ecuaciones y igualarlas.