Modelos matematicos para estudiar el virus de la influenza h1n1

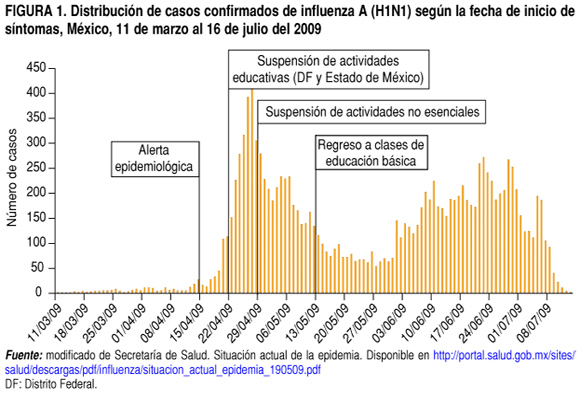
La influenza H1N1, también conocida como gripe porcina, es una enfermedad respiratoria que se propaga fácilmente de persona a persona. Desde su aparición en 2009, ha causado brotes en todo el mundo y ha sido motivo de preocupación para la salud pública.

Para entender mejor la propagación de la influenza H1N1, los científicos han desarrollado modelos matemáticos que pueden predecir la propagación del virus y ayudar a los profesionales de la salud a tomar medidas para controlar su propagación.

¿Qué son los modelos matemáticos?

Los modelos matemáticos son herramientas que nos permiten predecir el comportamiento de un sistema complejo utilizando ecuaciones y cálculos. En el caso de la influenza H1N1, los modelos matemáticos se utilizan para predecir cuántas personas se infectarán con el virus, cuánto tiempo durará la epidemia y cuántas personas necesitarán tratamiento médico.

Cómo funcionan los modelos matemáticos de la influenza H1N1

Los modelos matemáticos de la influenza H1N1 se basan en tres factores clave: la tasa de transmisión, la tasa de mortalidad y la tasa de recuperación. Estos factores se utilizan para crear ecuaciones que describen la propagación del virus.

Por ejemplo, una ecuación podría describir la tasa a la que se infectan las personas y otra ecuación podría describir la tasa a la que se recuperan. Al combinar estas ecuaciones, los científicos pueden predecir cuántas personas se infectarán, cuánto tiempo durará la epidemia y cuántas personas necesitarán tratamiento médico.

¿Cuáles son los beneficios de los modelos matemáticos?

Los modelos matemáticos de la influenza H1N1 tienen varios beneficios. En primer lugar, pueden ayudar a los profesionales de la salud a prepararse mejor para una epidemia. Al predecir cuántas personas se infectarán y cuántas necesitarán tratamiento médico, los hospitales y los sistemas de salud pueden prepararse para manejar un mayor número de pacientes.

En segundo lugar, los modelos matemáticos pueden ayudar a los gobiernos a tomar decisiones informadas sobre cómo controlar la propagación del virus. Al predecir cuánto tiempo durará la epidemia y cuántas personas se infectarán, los gobiernos pueden tomar medidas para limitar la propagación del virus, como cerrar escuelas y cancelar eventos públicos.

Comparación con tablas

Los modelos matemáticos de la influenza H1N1 se asemejan a las tablas en el sentido de que ambos utilizan datos para representar información. Sin embargo, mientras que las tablas se utilizan para presentar datos de manera organizada y visualmente atractiva, los modelos matemáticos se utilizan para predecir cómo se comportará un sistema en el futuro.

Preguntas frecuentes

¿Los modelos matemáticos son precisos?

Los modelos matemáticos de la influenza H1N1 son lo más precisos posible, pero no pueden predecir el futuro con certeza. Los modelos se basan en suposiciones y estimaciones, por lo que pueden haber factores imprevistos que afecten la propagación del virus.

¿Cómo se recopilan los datos necesarios para los modelos matemáticos?

Los datos utilizados en los modelos matemáticos de la influenza H1N1 se recopilan a través de diversas fuentes, como informes de hospitales y centros de salud, encuestas y datos de redes sociales.

¿Los modelos matemáticos solo se utilizan para la influenza H1N1?

No, los modelos matemáticos se utilizan en una variedad de campos, desde la física hasta la economía. En el campo de la salud, se utilizan para predecir la propagación de enfermedades como el VIH y el Ébola.

¿Cómo pueden los modelos matemáticos ayudar a prevenir futuras epidemias de influenza H1N1?

Los modelos matemáticos pueden ayudar a los profesionales de la salud y a los gobiernos a prepararse mejor para futuras epidemias de influenza H1N1 al proporcionar información sobre cómo se propagó el virus en el pasado y cómo se puede controlar en el futuro.

¿Los modelos matemáticos pueden reemplazar la investigación médica tradicional?

No, los modelos matemáticos no pueden reemplazar la investigación médica tradicional. Se utilizan en conjunto con la investigación médica para proporcionar una imagen completa de cómo se comporta una enfermedad y cómo se puede controlar.