Momento de una fuerza respecto a un eje problemas resueltos

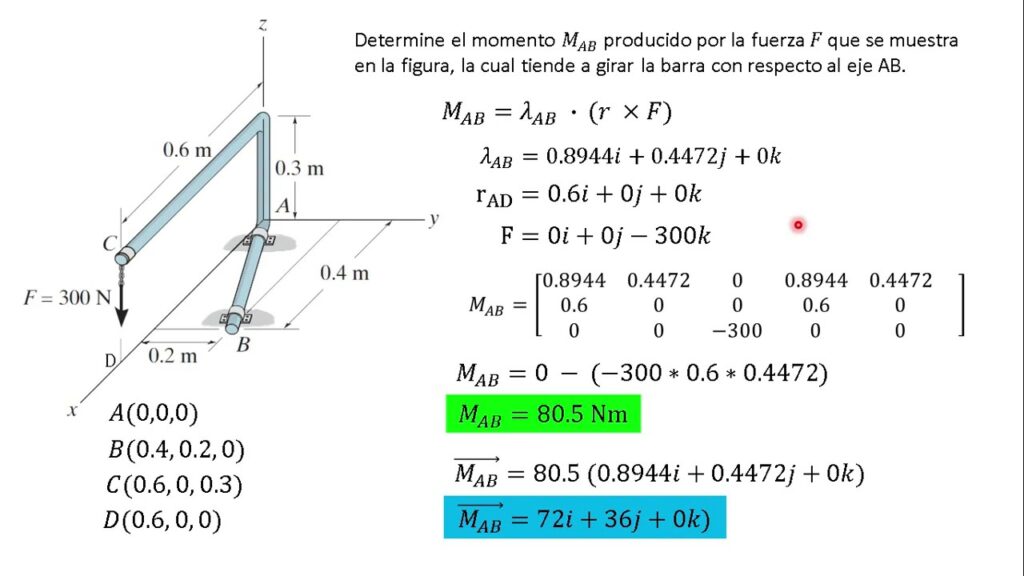
En física, el momento de una fuerza respecto a un eje es una magnitud que mide el efecto de una fuerza que actúa sobre un objeto en rotación. El momento de una fuerza se define como la magnitud del producto vectorial entre el vector de fuerza y el vector de posición del punto de aplicación de la fuerza respecto al eje de rotación. En este artículo, exploraremos algunos problemas resueltos sobre el momento de una fuerza respecto a un eje.

Problema 1:

Una varilla uniforme de 2 metros de longitud y 10 kg de masa está girando en torno a un eje que pasa por uno de sus extremos. Si la velocidad angular de la varilla es de 4 rad/s, ¿cuál es el momento de la fuerza necesaria para mantener la varilla en rotación?

Para resolver este problema, necesitamos recordar que el momento de una fuerza se define como el producto vectorial entre el vector de fuerza y el vector de posición del punto de aplicación de la fuerza respecto al eje de rotación. En este caso, la fuerza necesaria para mantener la varilla en rotación es la fuerza gravitatoria que actúa sobre la varilla, que se puede expresar como F = mg, donde m es la masa de la varilla y g es la aceleración gravitatoria.

El vector de posición del punto de aplicación de la fuerza respecto al eje de rotación es la distancia desde el extremo de la varilla hasta el centro de masa de la misma, que en este caso es igual a la mitad de la longitud de la varilla. Por lo tanto, el momento de la fuerza necesaria para mantener la varilla en rotación es:

M = F * d = (10 kg * 9,8 m/s^2) * 1 m = 98 Nm

Por lo tanto, se necesita una fuerza de 98 Nm para mantener la varilla en rotación.

Problema 2:

Una rueda de 0,5 metros de radio y 2 kg de masa está girando en torno a un eje que pasa por su centro con una velocidad angular de 10 rad/s. Si se aplica una fuerza de 20 N tangencialmente en el borde de la rueda, ¿cuál es el momento de la fuerza respecto al eje de rotación?

En este caso, la fuerza aplicada es tangencial al borde de la rueda, por lo que el vector de posición del punto de aplicación de la fuerza respecto al eje de rotación es igual al radio de la rueda. Por lo tanto, el momento de la fuerza es:

M = F * d = 20 N * 0,5 m = 10 Nm

Por lo tanto, el momento de la fuerza aplicada es de 10 Nm.

Problema 3:

Una puerta de 1,2 metros de ancho y 2 metros de altura está fijada a una pared mediante dos bisagras situadas a 0,2 metros del borde superior e inferior de la puerta. Si se aplica una fuerza de 50 N en el borde de la puerta, ¿cuál es el momento de la fuerza respecto al eje de rotación?

En este caso, el eje de rotación es la línea que une las dos bisagras. El vector de posición del punto de aplicación de la fuerza respecto al eje de rotación es la distancia desde el borde de la puerta hasta el eje de rotación, que en este caso es igual a la distancia desde el borde superior de la puerta hasta el eje de rotación, ya que la fuerza se aplica en ese punto. Por lo tanto, el momento de la fuerza es:

M = F * d = 50 N * 1 m = 50 Nm

Por lo tanto, el momento de la fuerza aplicada es de 50 Nm.

Problema 4:

Un disco uniforme de 3 kg de masa y 0,5 metros de radio está girando en torno a un eje que pasa por su centro con una velocidad angular de 6 rad/s. Si se aplica una fuerza de 10 N perpendicularmente al borde del disco, ¿cuál es el momento de la fuerza respecto al eje de rotación?

En este caso, la fuerza aplicada es perpendicular al borde del disco, por lo que el vector de posición del punto de aplicación de la fuerza respecto al eje de rotación es igual al radio del disco. Por lo tanto, el momento de la fuerza es:

M = F * d = 10 N * 0,5 m = 5 Nm

Por lo tanto, el momento de la fuerza aplicada es de 5 Nm.

Problema 5:

Una polea de 1 metro de diámetro y 5 kg de masa está girando en torno a un eje que pasa por su centro con una velocidad angular de 2 rad/s. Si se aplica una fuerza de 30 N tangencialmente en el borde de la polea, ¿cuál es el momento de la fuerza respecto al eje de rotación?

En este caso, la fuerza aplicada es tangencial al borde de la polea, por lo que el vector de posición del punto de aplicación de la fuerza respecto al eje de rotación es igual al radio de la polea. Por lo tanto, el momento de la fuerza es:

M = F * d = 30 N * 0,5 m = 15 Nm

Por lo tanto, el momento de la fuerza aplicada es de 15 Nm.

Conclusion

En conclusión, El momento de una fuerza respecto a un eje es una magnitud importante en física que mide el efecto de una fuerza que actúa sobre un objeto en rotación. Para calcular el momento de una fuerza, es necesario conocer el vector de fuerza y el vector de posición del punto de aplicación de la fuerza respecto al eje de rotación. Resolver problemas sobre el momento de una fuerza puede ayudarnos a entender mejor cómo se comportan los objetos en rotación y cómo las fuerzas afectan su movimiento.

Preguntas Frecuentes

1. ¿Qué es el momento de una fuerza?

El momento de una fuerza es una magnitud que mide el efecto de una fuerza que actúa sobre un objeto en rotación. Se define como el producto vectorial entre el vector de fuerza y el vector de posición del punto de aplicación de la fuerza respecto al eje de rotación.

2. ¿Cómo se calcula el momento de una fuerza?

El momento de una fuerza se calcula como el producto vectorial entre el vector de fuerza y el vector de posición del punto de aplicación de la fuerza respecto al eje de rotación.

3. ¿Qué es el vector de posición del punto de aplicación de la fuerza?

El vector de posición del punto de aplicación de la fuerza es la distancia desde el punto de aplicación de la fuerza hasta el eje de rotación. Este vector es importante para calcular el momento de una fuerza.

4. ¿Por qué es importante el momento de una fuerza?

El momento de una fuerza es importante porque nos ayuda a entender cómo se comportan los objetos en rotación y cómo las fuerzas afectan su movimiento. También es importante en muchas áreas de la física, como la mecánica clásica y la dinámica de fluidos.