Punto de interseccion de las tres alturas de un triangulo

Cuando hablamos de triángulos, existen una gran cantidad de conceptos y propiedades que se pueden analizar y estudiar. Uno de estos conceptos es el punto de intersección de las tres alturas de un triángulo, el cual es un tema importante en la geometría.

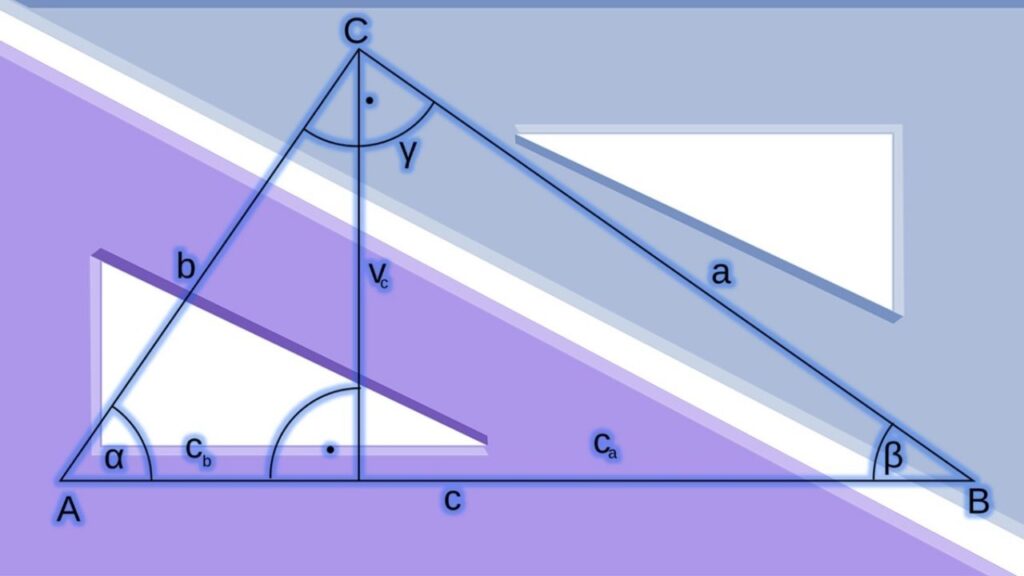
Las alturas de un triángulo son las líneas perpendiculares trazadas desde cada vértice del triángulo hasta su lado opuesto. El punto donde estas tres líneas se intersectan se conoce como el ortocentro del triángulo, y es el punto de intersección de las tres alturas del triángulo.

Para entender mejor este concepto, podemos compararlo con un edificio. Imagina que un edificio tiene tres pisos, y cada piso tiene un balcón que sobresale desde el edificio. Si trazamos una línea perpendicular desde cada balcón hasta el suelo, estas tres líneas se intersectarán en un solo punto. Este punto sería el punto de intersección de las alturas del edificio, y es similar al ortocentro de un triángulo.

El ortocentro de un triángulo puede estar dentro del triángulo, en el vértice del triángulo, o fuera del triángulo. Si el triángulo es acutángulo (todos sus ángulos son agudos), el ortocentro estará dentro del triángulo. Si el triángulo es rectángulo, el ortocentro estará en el vértice del ángulo recto. Y si el triángulo es obtusángulo (uno de sus ángulos es obtuso), el ortocentro estará fuera del triángulo.

Además, el ortocentro de un triángulo tiene algunas propiedades interesantes. Por ejemplo, las tres alturas del triángulo siempre se intersectan en el ortocentro, lo que significa que el ortocentro está en línea recta con cada vértice y el pie de cada altura. También es interesante notar que el ortocentro es el punto más cercano al triángulo de todas las rectas que pasan por cada vértice y son perpendiculares al lado opuesto.

En cuanto a su representación gráfica, es posible dibujar el ortocentro de un triángulo utilizando herramientas de geometría, como un compás y una regla. También se puede utilizar un software de geometría dinámica, como Geogebra, para visualizar el ortocentro y experimentar con diferentes triángulos.

En resumen, El punto de intersección de las tres alturas de un triángulo se conoce como el ortocentro del triángulo. Este punto puede estar dentro, en el vértice o fuera del triángulo, dependiendo del tipo de triángulo que se esté analizando. El ortocentro tiene algunas propiedades interesantes y puede ser representado gráficamente utilizando herramientas de geometría.

¿Qué es una altura en un triángulo?

En un triángulo, la altura es una línea perpendicular trazada desde un vértice del triángulo hasta el lado opuesto. Esta línea divide al triángulo en dos triángulos más pequeños y forma un ángulo recto con el lado opuesto. Cada triángulo tiene tres alturas, una desde cada vértice.

¿Qué es un triángulo acutángulo?

Un triángulo acutángulo es aquel que tiene todos sus ángulos agudos, es decir, menores a 90 grados. En este tipo de triángulo, el ortocentro estará dentro del triángulo.

¿Qué es un triángulo rectángulo?

Un triángulo rectángulo es aquel que tiene un ángulo recto, es decir, un ángulo de 90 grados. En este tipo de triángulo, el ortocentro estará en el vértice del ángulo recto.

¿Qué es un triángulo obtusángulo?

Un triángulo obtusángulo es aquel que tiene un ángulo obtuso, es decir, un ángulo mayor a 90 grados. En este tipo de triángulo, el ortocentro estará fuera del triángulo.

¿Cómo se puede encontrar el ortocentro de un triángulo?

El ortocentro de un triángulo se puede encontrar mediante la intersección de las tres alturas del triángulo. Estas alturas se pueden trazar utilizando un compás y una regla, o mediante herramientas de geometría dinámica como Geogebra.