Que es el limite de una funcion en calculo diferencial

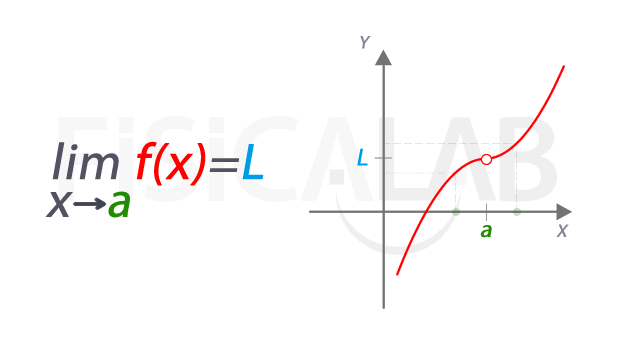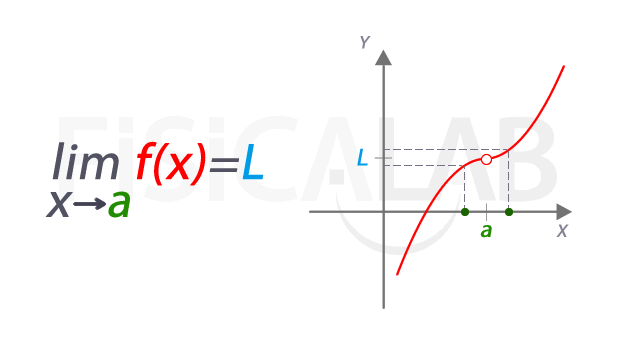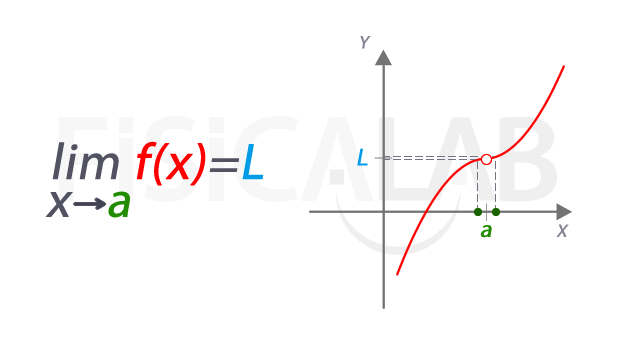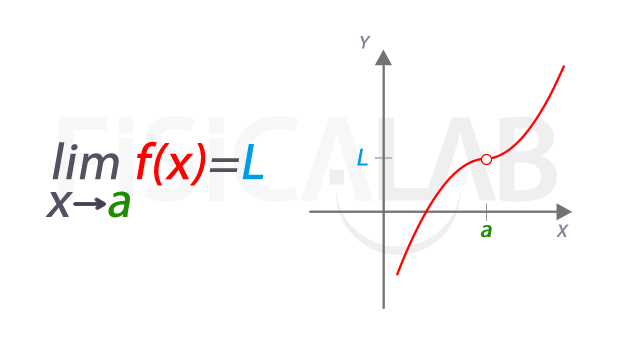
El límite de una función en cálculo diferencial es un concepto fundamental que se utiliza para entender el comportamiento de una función en un punto específico. En términos simples, el límite de una función se refiere al valor al que se acerca la función cuando su variable independiente se acerca a un valor específico, pero no necesariamente igual a ese valor. En otras palabras, el límite de una función describe el comportamiento de la función en un punto específico, pero no necesariamente en el punto mismo.

Cómo se calcula el límite de una función

Para calcular el límite de una función, es necesario analizar el comportamiento de la función a medida que su variable independiente se acerca a un valor específico. Si la función se acerca a un valor único cuando su variable independiente se acerca a ese valor específico, entonces se dice que la función tiene un límite en ese punto.

Por ejemplo, consideremos la función f(x) = (x^2 - 1)/(x - 1). Si evaluamos la función para valores cercanos a x = 1, obtenemos los siguientes resultados:

x = 0.9: f(0.9) = 1.9
x = 0.99: f(0.99) = 1.99
x = 0.999: f(0.999) = 1.999
x = 1.01: f(1.01) = 2.01
x = 1.1: f(1.1) = 2.1

Observamos que a medida que x se acerca a 1, la función f(x) se acerca a 2. Sin embargo, en x = 1, la función no está definida (ya que hay una división por cero). Por lo tanto, podemos decir que el límite de f(x) cuando x se acerca a 1 es igual a 2.

Qué significa un límite que no existe

En algunos casos, el límite de una función puede no existir en un punto específico. Esto ocurre cuando la función se acerca a diferentes valores cuando su variable independiente se acerca a ese punto desde diferentes direcciones. Por ejemplo, consideremos la función g(x) = sin(1/x). Si evaluamos la función para valores cercanos a x = 0, obtenemos los siguientes resultados:

x = 0.1: g(0.1) = sin(10)
x = 0.01: g(0.01) = sin(100)
x = 0.001: g(0.001) = sin(1000)
x = -0.1: g(-0.1) = sin(-10)
x = -0.01: g(-0.01) = sin(-100)
x = -0.001: g(-0.001) = sin(-1000)

Observamos que la función oscila entre -1 y 1 a medida que x se acerca a 0 desde diferentes direcciones. En este caso, decimos que el límite de g(x) cuando x se acerca a 0 no existe.

Por qué es importante el límite de una función

El límite de una función es importante porque nos permite entender el comportamiento de la función en un punto específico. Este concepto es fundamental en muchas áreas de las matemáticas y la física, ya que nos permite calcular derivadas, integrales, tasas de cambio y muchas otras cantidades importantes.

Por ejemplo, para calcular la derivada de una función en un punto específico, es necesario calcular el límite de la función a medida que su variable independiente se acerca a ese punto. La derivada de una función describe la tasa de cambio instantánea de la función en ese punto, y es fundamental en muchos campos de la física y la ingeniería.

Comparación con tablas y listas

En términos de programación web, el límite de una función se puede comparar con las tablas y las listas. Al igual que el límite de una función describe el comportamiento de la función en un punto específico, las tablas y las listas describen la estructura de los datos en una página web.

Las tablas se utilizan para mostrar datos en una cuadrícula, donde cada fila representa un registro y cada columna representa un campo de datos. Por otro lado, las listas se utilizan para mostrar datos en una lista, donde cada elemento representa un registro y cada atributo representa un campo de datos.

Al igual que el límite de una función es fundamental para comprender el comportamiento de la función en un punto específico, las tablas y las listas son fundamentales para comprender la estructura de los datos en una página web.

Preguntas frecuentes

¿Por qué es importante calcular el límite de una función?

El límite de una función es importante porque nos permite entender el comportamiento de la función en un punto específico. Este concepto es fundamental en muchas áreas de las matemáticas y la física, ya que nos permite calcular derivadas, integrales, tasas de cambio y muchas otras cantidades importantes.

¿Qué significa un límite que no existe?

En algunos casos, el límite de una función puede no existir en un punto específico. Esto ocurre cuando la función se acerca a diferentes valores cuando su variable independiente se acerca a ese punto desde diferentes direcciones.

¿Cómo se calcula el límite de una función?

Para calcular el límite de una función, es necesario analizar el comportamiento de la función a medida que su variable independiente se acerca a un valor específico. Si la función se acerca a un valor único cuando su variable independiente se acerca a ese valor específico, entonces se dice que la función tiene un límite en ese punto.

¿Por qué es importante el límite de una función en la física?

El límite de una función es importante en la física porque nos permite calcular tasas de cambio instantáneas, que son fundamentales para comprender el comportamiento de los sistemas físicos. Por ejemplo, la velocidad instantánea de un objeto se puede calcular como la derivada de su posición en función del tiempo, que a su vez se puede calcular como el límite de la función de posición cuando el tiempo se acerca a un valor específico.

¿Qué es una tabla HTML?

Una tabla HTML es una estructura de datos en forma de cuadrícula que se utiliza para mostrar información en una página web. Cada fila representa un registro y cada columna representa un campo de datos. Las tablas se utilizan comúnmente para mostrar datos en forma de hojas de cálculo o bases de datos.