Que es la aplicacion sucesiva de factores constantes de proporcionalidad

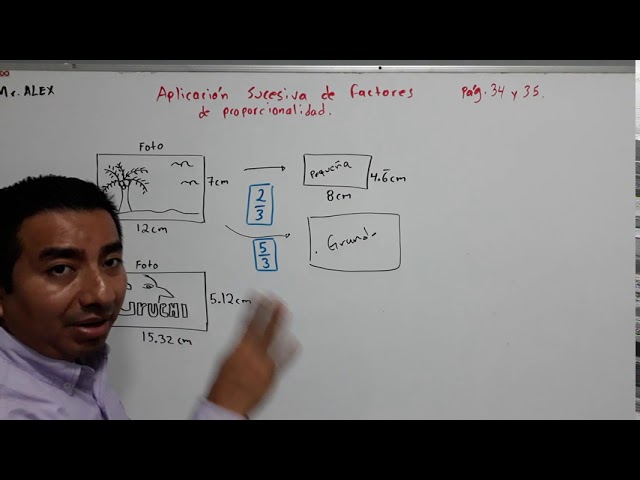
En matemáticas, la proporcionalidad es una relación entre dos magnitudes que se pueden expresar como una fracción o razón. Si multiplicamos o dividimos una de las magnitudes por un número constante, la relación de proporcionalidad entre ellas sigue siendo la misma. La aplicación sucesiva de factores constantes de proporcionalidad se refiere a multiplicar o dividir ambas magnitudes por un número constante varias veces.

Por ejemplo, si tenemos una proporción entre dos magnitudes A y B, podemos expresarla como A/B = k, donde k es una constante de proporcionalidad. Si multiplicamos ambas magnitudes por un número constante c, la relación de proporcionalidad sigue siendo la misma: (cA)/(cB) = A/B = k. Si ahora multiplicamos la proporción resultante por otro número constante d, obtenemos (cdA)/(cdB) = A/B = k. Este proceso se puede repetir varias veces, multiplicando o dividiendo ambas magnitudes por números constantes diferentes.

La aplicación sucesiva de factores constantes de proporcionalidad se utiliza en diversas áreas de las matemáticas y la física. Por ejemplo, en la ley de gravitación de Newton, la fuerza de atracción entre dos objetos es proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia entre ellos. Si tenemos tres objetos con masas m1, m2 y m3 y distancias r12, r13 y r23 entre ellos, la fuerza resultante sobre el objeto 1 será proporcional a (m1m2)/(r12^2), (m1m3)/(r13^2) y (m2m3)/(r23^2). Si aplicamos factores constantes de proporcionalidad a estas magnitudes, podemos simplificar la expresión resultante y obtener una fórmula más sencilla para la fuerza total sobre el objeto 1.

Las tablas son una forma útil de comparar diferentes valores de magnitudes que están relacionadas por proporciones. Por ejemplo, si queremos comparar los precios de diferentes productos que se venden en diferentes cantidades, podemos usar una tabla HTML para mostrar el precio por unidad de cada producto. En la tabla, las magnitudes de precio y cantidad se relacionan por una constante de proporcionalidad, y podemos aplicar factores constantes para obtener el precio por unidad de diferentes cantidades.

Algunas preguntas frecuentes sobre la aplicación sucesiva de factores constantes de proporcionalidad son:

1. ¿Por qué es importante la proporcionalidad en matemáticas y física?
La proporcionalidad es una herramienta fundamental para entender cómo se relacionan diferentes magnitudes en el mundo real. Muchas leyes y principios de la física se basan en relaciones de proporcionalidad, y la capacidad de identificar y aplicar estas relaciones es esencial para resolver problemas matemáticos y científicos.

2. ¿Cómo se aplica la proporcionalidad en la vida cotidiana?
La proporcionalidad se utiliza en muchas situaciones cotidianas, como calcular el precio por unidad de diferentes productos en un supermercado, determinar la cantidad de ingredientes necesarios para una receta, o ajustar la velocidad de un vehículo para mantener una distancia segura con otros vehículos.

3. ¿Qué ocurre si no se aplican factores constantes de proporcionalidad correctamente?
Si no se aplican factores constantes de proporcionalidad correctamente, se pueden obtener resultados incorrectos o incoherentes. Es importante asegurarse de que las magnitudes que se comparan están en la misma unidad y que se están aplicando los factores correctos para mantener la relación de proporcionalidad constante.

4. ¿Qué otras herramientas matemáticas se utilizan junto con la proporcionalidad?
La proporcionalidad se utiliza junto con otras herramientas matemáticas como las funciones lineales, las ecuaciones y los gráficos para resolver problemas matemáticos y científicos. Estas herramientas permiten representar y manipular relaciones de proporcionalidad de manera más precisa y eficiente.

5. ¿Cómo se pueden aplicar las proporciones en la vida real?
Las proporciones se utilizan en muchas situaciones de la vida real, como calcular el porcentaje de descuento en una oferta de compra, determinar la cantidad de agua necesaria para diluir una solución, o comparar los precios de diferentes planes de teléfono móvil. La capacidad de identificar y aplicar relaciones de proporcionalidad es esencial para tomar decisiones informadas y realizar cálculos precisos en muchas áreas de la vida.