Que es la media aritmetica la moda y la mediana
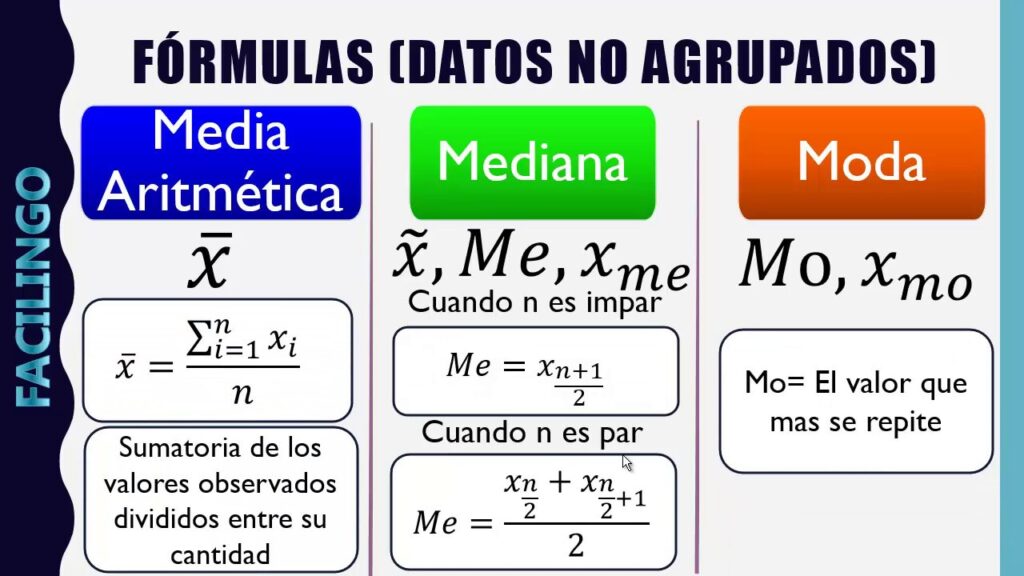
Cuando se habla de estadísticas, hay tres términos que suelen aparecer con frecuencia: la media aritmética, la moda y la mediana. Cada uno de estos conceptos es una herramienta útil para analizar datos y entender la distribución de un conjunto de números. En este artículo, explicaremos en qué consiste cada uno de ellos y cómo se calculan.
La media aritmética
La media aritmética es el término más conocido de los tres. Se trata de un valor que representa el promedio de un conjunto de números. Para calcular la media aritmética, se suman todos los valores y se dividen entre la cantidad de elementos. Por ejemplo, si tenemos un conjunto de números {2, 4, 6, 8, 10}, la media aritmética sería:
(2 + 4 + 6 + 8 + 10) / 5 = 6
La media aritmética es una buena herramienta para obtener una idea general de la distribución de los datos. Sin embargo, tiene una limitación: puede verse afectada por valores atípicos (outliers) en el conjunto de datos. Por ejemplo, si en el conjunto anterior añadiéramos un 20, la media aritmética aumentaría a 8, y no reflejaría la mayoría de los valores del conjunto.
La moda
La moda es el valor que aparece con mayor frecuencia en un conjunto de datos. Para encontrar la moda, basta con contar cuántas veces aparece cada número y ver cuál es el que se repite más veces. En algunos casos, puede haber más de una moda, si dos o más valores aparecen con la misma frecuencia.
Por ejemplo, en el conjunto de números {2, 4, 6, 8, 8, 10}, la moda sería 8, ya que es el valor que aparece dos veces, mientras que los demás solo aparecen una vez.
La moda es especialmente útil cuando se trabaja con datos discretos, es decir, números enteros que representan categorías o grupos. Por ejemplo, si se está analizando la frecuencia de uso de diferentes palabras en un texto, la moda puede indicar cuál es la palabra más común.
La mediana
La mediana es el valor que se encuentra en el punto medio de un conjunto de datos ordenados. Para encontrar la mediana, primero se ordenan los datos de menor a mayor (o viceversa), y luego se busca el valor que está justo en el centro. Si el conjunto tiene un número par de elementos, se toma la media aritmética de los dos valores del centro.
Por ejemplo, en el conjunto de números {2, 4, 6, 8, 10}, la mediana sería 6, ya que es el valor que está justo en el medio de la secuencia ordenada.
La mediana es una buena herramienta para analizar conjuntos de datos que tienen valores atípicos o que no siguen una distribución normal. Aunque la mediana no se ve afectada por valores extremos, puede no reflejar la mayoría de los datos, especialmente si el conjunto tiene una distribución sesgada.
Comparación entre los tres conceptos
La siguiente tabla muestra las diferencias entre la media aritmética, la moda y la mediana:
| Media aritmética | Moda | Mediana | |
|---|---|---|---|
| Definición | Promedio de un conjunto de números | Valor que aparece con mayor frecuencia | Valor que se encuentra en el punto medio de un conjunto de datos ordenados |
| Uso | Obtener una idea general de la distribución de los datos | Analizar la frecuencia de valores discretos | Analizar conjuntos de datos con valores atípicos o sesgos |
| Limitaciones | Puede verse afectada por valores atípicos | No es útil para datos continuos | No refleja la mayoría de los datos si el conjunto tiene una distribución sesgada |
Preguntas frecuentes
¿Qué es un valor atípico?
Un valor atípico (o outlier) es un número que se aleja significativamente del resto de los datos en un conjunto. Los valores atípicos pueden afectar la media aritmética y distorsionar la interpretación de los datos.
¿Por qué la moda no es útil para datos continuos?
La moda se basa en la frecuencia de los valores en un conjunto de datos. En datos continuos, es poco probable que dos valores tengan exactamente la misma frecuencia, lo que hace que la moda no sea una herramienta útil para analizar la distribución de los datos.
¿Cuál es la diferencia entre la media aritmética y la media ponderada?
La media aritmética es el promedio simple de un conjunto de números, mientras que la media ponderada asigna pesos a cada valor y calcula el promedio en función de esos pesos. La media ponderada es útil cuando algunos valores son más importantes que otros en el conjunto de datos.
¿La mediana siempre es un valor del conjunto de datos?
No necesariamente. En algunos casos, la mediana puede ser un valor que no aparece en el conjunto de datos, especialmente si el conjunto tiene un número par de elementos.
¿Qué es una distribución sesgada?
Una distribución sesgada es aquella en la que la mayoría de los datos se concentran en un extremo del conjunto, y hay pocos valores en el otro extremo. Una distribución sesgada puede afectar la interpretación de la media aritmética y la mediana, ya que estas medidas pueden no reflejar la mayoría de los datos.

Deja una respuesta