Que es un sistema de ecuaciones lineales con 2 variables
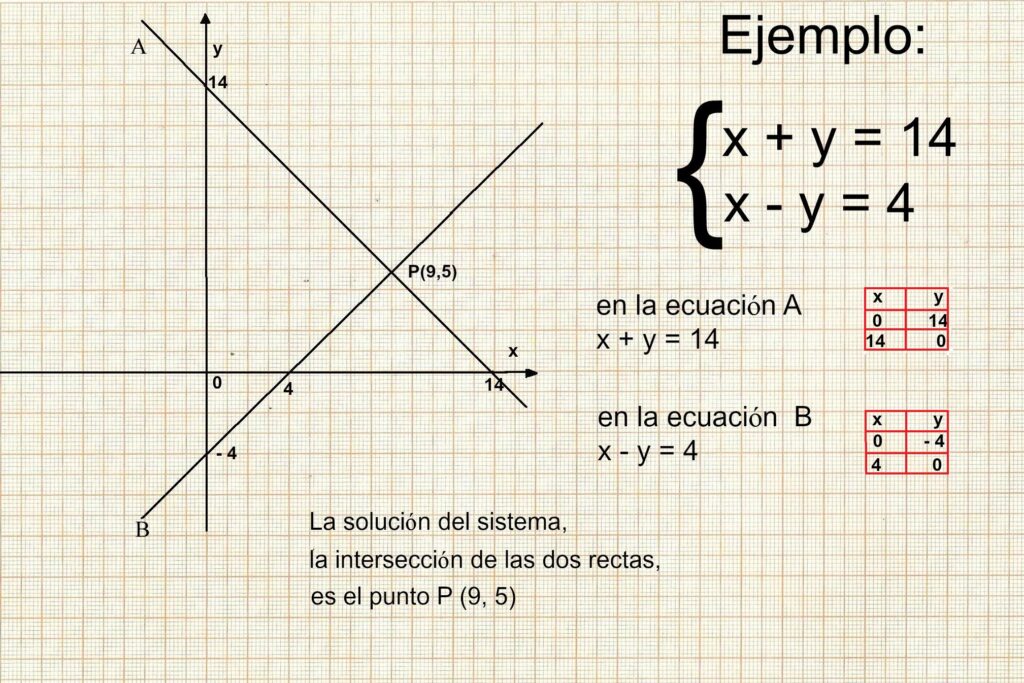
Cuando hablamos de sistemas de ecuaciones lineales con 2 variables, nos referimos a una serie de ecuaciones que tienen dos variables desconocidas. Estas ecuaciones están relacionadas entre sí y pueden ser resueltas de manera simultánea para encontrar los valores de las variables.
Un sistema de ecuaciones lineales con 2 variables puede ser representado de diferentes maneras, pero la más común es utilizando la notación matricial. En este caso, el sistema se escribe como:
Ax + By = C
Dx + Ey = F
Donde A, B, D y E son los coeficientes de las variables x e y, mientras que C y F son los términos independientes. Para resolver este sistema, se puede utilizar el método de sustitución o el método de eliminación.
El método de sustitución implica despejar una de las variables de una de las ecuaciones y sustituirla en la otra ecuación. Esto nos dará una ecuación con una sola variable, que podemos resolver para encontrar su valor. Una vez que conocemos el valor de una de las variables, podemos sustituirlo en cualquiera de las dos ecuaciones originales y encontrar el valor de la otra variable.
El método de eliminación, por otro lado, implica sumar o restar ambas ecuaciones de manera que una de las variables se elimine. Esto nos dará una ecuación con una sola variable, que podemos resolver para encontrar su valor. Una vez que conocemos el valor de una de las variables, podemos sustituirlo en cualquiera de las dos ecuaciones originales y encontrar el valor de la otra variable.
En términos prácticos, podemos pensar en un sistema de ecuaciones lineales con 2 variables como un juego de equilibrio. Imagina que tienes dos platos de comida y necesitas saber cuánta comida hay en cada plato para asegurarte de que ambos tengan la misma cantidad. Para resolver este problema, podrías utilizar un sistema de ecuaciones lineales con 2 variables, donde las dos variables desconocidas son la cantidad de comida en cada plato. Al resolver el sistema, podrías determinar la cantidad exacta de comida que necesitas agregar o quitar para lograr el equilibrio.
Las tablas son una excelente herramienta para comparar y visualizar los resultados de un sistema de ecuaciones lineales con 2 variables. Por ejemplo, si estamos resolviendo el siguiente sistema:
2x + 3y = 7
-4x + 5y = 8
Podríamos utilizar una tabla HTML para organizar los coeficientes y términos independientes de cada ecuación:
| x | y | |
|---|---|---|
| 2 | 3 | = 7 |
| -4 | 5 | = 8 |
Una vez que hemos organizado los datos en la tabla, podemos utilizar el método de eliminación para resolver el sistema. En este caso, podemos multiplicar la primera ecuación por 2 y sumarla a la segunda ecuación para eliminar la variable x:
4x + 6y = 14
-4x + 5y = 8
11y = 22
y = 2
Ahora que conocemos el valor de y, podemos sustituirlo en cualquiera de las dos ecuaciones originales y encontrar el valor de x:
2x + 3(2) = 7
2x + 6 = 7
2x = 1
x = 0.5
Por lo tanto, la solución del sistema de ecuaciones lineales con 2 variables es x = 0.5 y y = 2.
En conclusión, Un sistema de ecuaciones lineales con 2 variables es un conjunto de ecuaciones que tienen dos variables desconocidas. Estas ecuaciones están relacionadas entre sí y pueden ser resueltas de manera simultánea utilizando el método de sustitución o el método de eliminación. Las tablas son una herramienta útil para comparar y visualizar los resultados de un sistema de ecuaciones lineales con 2 variables. Al comprender cómo resolver sistemas de ecuaciones lineales con 2 variables, podemos aplicar estos conceptos en situaciones prácticas de la vida cotidiana.
Preguntas frecuentes:
1. ¿Cuál es la diferencia entre un sistema de ecuaciones lineales con 2 variables y un sistema de ecuaciones lineales con 3 variables?
R: Un sistema de ecuaciones lineales con 2 variables tiene dos variables desconocidas, mientras que un sistema de ecuaciones lineales con 3 variables tiene tres variables desconocidas.
2. ¿Qué sucede si el sistema de ecuaciones lineales con 2 variables no tiene solución?
R: Si el sistema no tiene solución, significa que las dos ecuaciones no son compatibles y no hay valores que satisfagan ambas ecuaciones simultáneamente.
3. ¿Qué sucede si el sistema de ecuaciones lineales con 2 variables tiene infinitas soluciones?
R: Si el sistema tiene infinitas soluciones, significa que las dos ecuaciones son equivalentes y representan la misma línea en un plano cartesiano.
4. ¿Cuál es el método más eficiente para resolver un sistema de ecuaciones lineales con 2 variables?
R: El método más eficiente dependerá de las características del sistema en particular. En algunos casos, el método de sustitución puede ser más eficiente, mientras que en otros casos el método de eliminación puede ser más rápido.
5. ¿En qué campos se utiliza la resolución de sistemas de ecuaciones lineales con 2 variables?
R: La resolución de sistemas de ecuaciones lineales con 2 variables es utilizada en campos como la física, la ingeniería, las ciencias económicas y la estadística, entre otros.

Deja una respuesta