Sea el triangulo formado por tres puntos cuyas coordenadas son

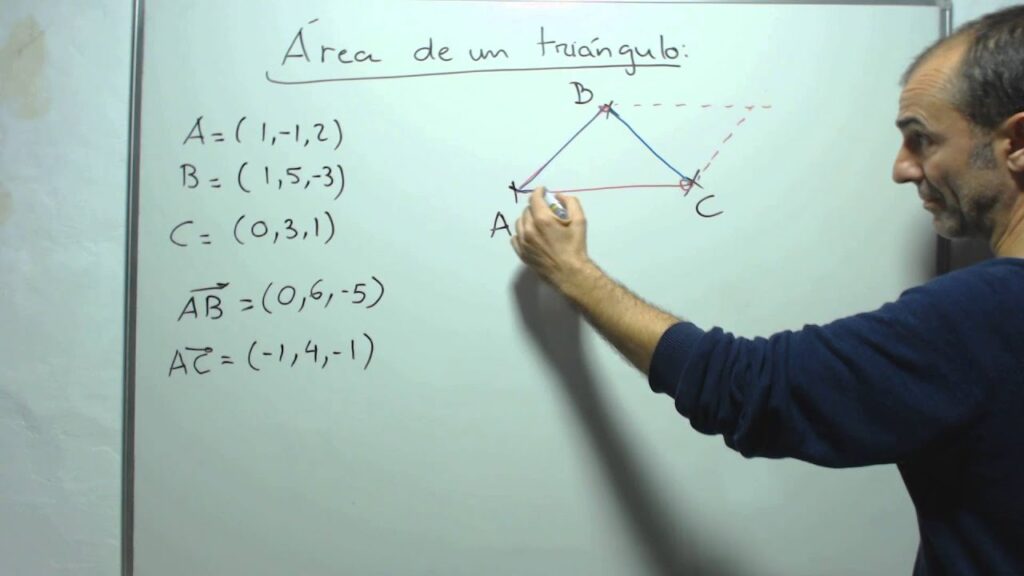
En la geometría, el triángulo es una figura básica que se forma a partir de tres puntos no colineales en el plano. Cada uno de estos puntos tiene una coordenada en el sistema de coordenadas cartesianas (x, y), lo que permite conocer su posición exacta. En este artículo, hablaremos sobre cómo se puede formar un triángulo a partir de las coordenadas de tres puntos y cuáles son las propiedades que se pueden derivar de ellos.

¿Cómo se puede determinar el área de un triángulo a partir de sus coordenadas?

Para calcular el área de un triángulo, se necesita conocer la base y la altura del mismo. En el caso de un triángulo definido por tres puntos en un plano, se puede encontrar la base midiendo la distancia entre dos de los puntos y la altura midiendo la distancia desde el tercer punto a la línea que une los otros dos.

La fórmula para calcular el área de un triángulo a partir de sus coordenadas es la siguiente:

Área = 1/2 * |(x1 * (y2 - y3) + x2 * (y3 - y1) + x3 * (y1 - y2))|

Donde x1, y1, x2, y2, x3, y3 son las coordenadas de los tres puntos.

¿Cómo se puede determinar si un triángulo es equilátero, isósceles o escaleno?

Un triángulo equilátero es aquel en el que los tres lados tienen la misma longitud. Un triángulo isósceles es aquel en el que dos lados tienen la misma longitud y el tercero es diferente. Un triángulo escaleno es aquel en el que los tres lados tienen longitudes diferentes.

Para determinar si un triángulo es equilátero, isósceles o escaleno a partir de sus coordenadas, se puede medir la longitud de sus lados utilizando la fórmula de distancia entre dos puntos. Si los tres lados tienen la misma longitud, el triángulo es equilátero. Si dos lados tienen la misma longitud y el tercero es diferente, el triángulo es isósceles. Si los tres lados tienen longitudes diferentes, el triángulo es escaleno.

¿Cómo se puede determinar si un triángulo es rectángulo?

Un triángulo rectángulo es aquel en el que uno de sus ángulos es un ángulo recto (90 grados). Para determinar si un triángulo es rectángulo a partir de sus coordenadas, se puede utilizar el teorema de Pitágoras. Si la suma de los cuadrados de dos de los lados es igual al cuadrado del tercer lado, entonces el triángulo es rectángulo.

¿Cómo se puede determinar si un punto está dentro de un triángulo?

Para determinar si un punto está dentro de un triángulo a partir de sus coordenadas, se puede utilizar el método del signo del área. Este método se basa en el hecho de que el área de un triángulo es siempre positiva, por lo que si un punto está dentro del triángulo, las áreas de los triángulos formados por el punto y cada par de vértices del triángulo tendrán el mismo signo. Si el punto está fuera del triángulo, las áreas tendrán signos opuestos.

¿Cómo se puede representar un triángulo en una tabla HTML?

En una tabla HTML, se puede representar un triángulo utilizando las etiquetas de celda (td) y fila (tr) y estableciendo el ancho y la altura de las celdas para que formen la forma de un triángulo. Por ejemplo, el siguiente código muestra cómo representar un triángulo equilátero en una tabla HTML:

```

```

En este ejemplo, hay dos filas y tres celdas en la primera fila y dos celdas en la segunda fila. Al establecer el ancho y la altura de las celdas correctamente, se puede formar un triángulo equilátero.

Conclusión

En resumen, Las coordenadas de tres puntos en un plano pueden utilizarse para formar un triángulo y calcular su área, así como para determinar si es equilátero, isósceles, escaleno o rectángulo. Además, se puede utilizar el método del signo del área para determinar si un punto está dentro de un triángulo. En una tabla HTML, se puede representar un triángulo utilizando las etiquetas de celda y fila y estableciendo el ancho y la altura de las celdas para formar la forma deseada.

Preguntas frecuentes

1. ¿Por qué es importante conocer las coordenadas de los puntos para formar un triángulo?

Es importante conocer las coordenadas de los puntos para formar un triángulo porque esto permite calcular su área y determinar sus propiedades, como si es equilátero, isósceles o escaleno. Además, las coordenadas pueden utilizarse para determinar si un punto está dentro o fuera del triángulo.

2. ¿Cómo se puede calcular la altura de un triángulo a partir de sus coordenadas?

Para calcular la altura de un triángulo a partir de sus coordenadas, se puede medir la distancia desde el tercer punto a la línea que une los otros dos puntos. Esta distancia es la altura del triángulo.

3. ¿Cómo se puede determinar si dos triángulos son congruentes a partir de sus coordenadas?

Dos triángulos son congruentes si tienen los mismos lados y ángulos. Para determinar si dos triángulos son congruentes a partir de sus coordenadas, se puede comparar la longitud de sus lados y el tamaño de sus ángulos utilizando las fórmulas correspondientes.

4. ¿Cómo se puede encontrar el perímetro de un triángulo a partir de sus coordenadas?

Para encontrar el perímetro de un triángulo a partir de sus coordenadas, se puede medir la longitud de cada uno de sus lados utilizando la fórmula de distancia entre dos puntos y luego sumar estas longitudes.

5. ¿Cómo se puede utilizar el teorema de Pitágoras para determinar si un triángulo es rectángulo?

El teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las longitudes de los otros dos lados. Para determinar si un triángulo es rectángulo a partir de sus coordenadas, se puede utilizar esta fórmula y comprobar si se cumple esta relación.