Sustitucion trigonometrica de acuerdo a la forma de la raiz

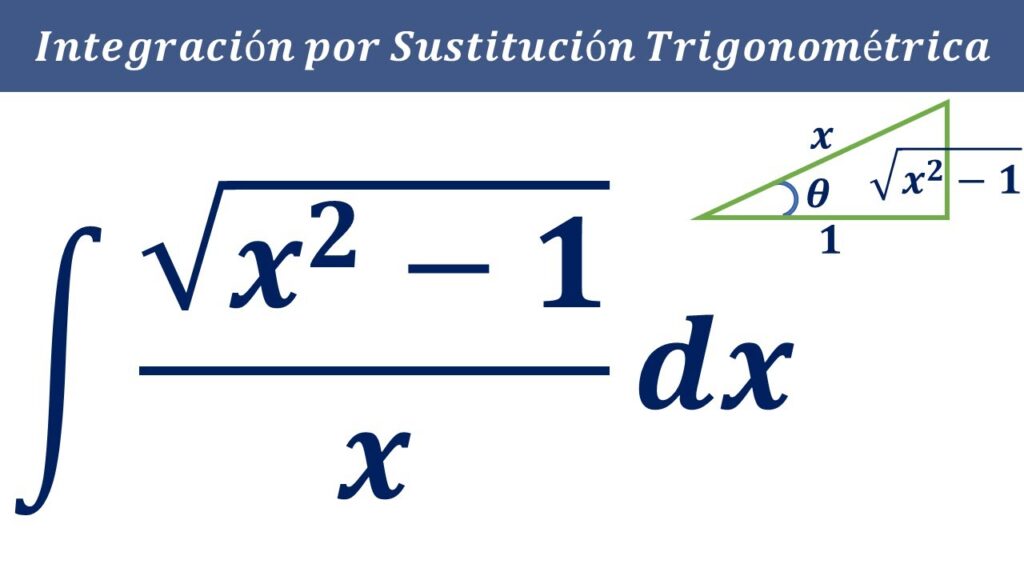
La sustitución trigonométrica es una técnica muy útil para resolver integrales en las que aparecen raíces cuadradas. La idea detrás de esta técnica es sustituir la expresión dentro de la raíz por una función trigonométrica que la simplifique y permita su integración. En este artículo, nos enfocaremos en la sustitución trigonométrica según la forma de la raíz.

Forma cuadrada perfecta

Cuando la expresión dentro de la raíz es un cuadrado perfecto, es decir, puede ser escrito como el cuadrado de una expresión algebraica, se utiliza la siguiente sustitución:

$$sqrt{a^2-x^2}to asin(t)$$

En este caso, se sustituye $x$ por $asin(t)$ y se resuelve para $dx$. Después, se reemplaza en la integral original y se simplifica usando identidades trigonométricas.

Ejemplo:

$$intsqrt{16-x^2}dx$$

En este caso, $a=4$, por lo que la sustitución es $x=4sin(t)$ y $dx=4cos(t)dt$. Sustituyendo en la integral original, obtenemos:

$$intsqrt{16-16sin^2(t)}4cos(t)dt=int4cos^2(t)dt$$

Usando la identidad trigonométrica $cos^2(t)=frac{1+cos(2t)}{2}$, podemos simplificar la integral a:

$$intfrac{1}{2}(4+4cos(2t))dt=2t+sin(2t)+C$$

Sustituyendo de regreso $t=arcsinleft(frac{x}{4}right)$, obtenemos la solución final:

$$intsqrt{16-x^2}dx=2arcsinleft(frac{x}{4}right)+frac{x}{2}sqrt{16-x^2}+C$$

Forma $a^2+x^2$

Cuando la expresión dentro de la raíz es de la forma $a^2+x^2$, se utiliza la siguiente sustitución:

$$sqrt{a^2+x^2}to atan(t)$$

En este caso, se sustituye $x$ por $atan(t)$ y se resuelve para $dx$. Después, se reemplaza en la integral original y se simplifica usando identidades trigonométricas.

Ejemplo:

$$intfrac{1}{sqrt{4+x^2}}dx$$

En este caso, $a=2$, por lo que la sustitución es $x=2tan(t)$ y $dx=2sec^2(t)dt$. Sustituyendo en la integral original, obtenemos:

$$intfrac{2sec^2(t)}{sqrt{4+4tan^2(t)}}dt=intfrac{2sec^2(t)}{2sec(t)}dt=int2cos(t)dt$$

La integral resultante se puede resolver fácilmente y la solución final es:

$$intfrac{1}{sqrt{4+x^2}}dx=arcsinleft(frac{x}{2}right)+C$$

Forma $a^2-x^2$

Cuando la expresión dentro de la raíz es de la forma $a^2-x^2$, se utiliza la siguiente sustitución:

$$sqrt{a^2-x^2}to acos(t)$$

En este caso, se sustituye $x$ por $asin(t)$ y se resuelve para $dx$. Después, se reemplaza en la integral original y se simplifica usando identidades trigonométricas.

Ejemplo:

$$intfrac{x^2}{sqrt{9-x^2}}dx$$

En este caso, $a=3$, por lo que la sustitución es $x=3sin(t)$ y $dx=3cos(t)dt$. Sustituyendo en la integral original, obtenemos:

$$intfrac{9sin^2(t)}{3cos(t)}3cos(t)dt=3intsin^2(t)dt$$

Usando la identidad trigonométrica $sin^2(t)=frac{1-cos(2t)}{2}$, podemos simplificar la integral a:

$$3intfrac{1-cos(2t)}{2}dt=frac{3}{2}t-frac{3}{4}sin(2t)+C$$

Sustituyendo de regreso $t=arcsinleft(frac{x}{3}right)$, obtenemos la solución final:

$$intfrac{x^2}{sqrt{9-x^2}}dx=frac{3}{2}arcsinleft(frac{x}{3}right)-frac{3}{4}xsqrt{9-x^2}+C$$

Conclusión

La sustitución trigonométrica es una técnica muy útil para resolver integrales que involucran raíces cuadradas. Dependiendo de la forma de la raíz, se puede elegir la sustitución adecuada para simplificar la integral y permitir su resolución. Es importante recordar que después de aplicar la sustitución, se deben simplificar las expresiones usando identidades trigonométricas y reemplazar de regreso para obtener la solución final.

Preguntas frecuentes

¿Por qué se utiliza la sustitución trigonométrica?

La sustitución trigonométrica es una técnica útil para resolver integrales que involucran raíces cuadradas. Al sustituir la expresión dentro de la raíz por una función trigonométrica, es posible simplificar la integral y permitir su resolución.

¿Cómo se elige la sustitución adecuada?

La elección de la sustitución adecuada depende de la forma de la raíz. En general, se utilizan las siguientes sustituciones: $asin(t)$ para la forma cuadrada perfecta, $atan(t)$ para la forma $a^2+x^2$ y $acos(t)$ para la forma $a^2-x^2$.

¿Cómo se resuelve la integral después de aplicar la sustitución?

Después de aplicar la sustitución trigonométrica, se debe resolver la integral sustituyendo la expresión trigonométrica obtenida y su derivada en la integral original. Luego, se simplifica la expresión usando identidades trigonométricas y se reemplaza de regreso para obtener la solución final.

¿Qué son las identidades trigonométricas?

Las identidades trigonométricas son relaciones matemáticas entre las funciones trigonométricas seno, coseno y tangente. Estas relaciones se utilizan para simplificar expresiones y resolver integrales que involucran funciones trigonométricas.

¿Qué son las tablas y cómo se usan?

Las tablas son elementos que se utiliz