Una figura que tenga 8 1/2 unidades cuadradas de area
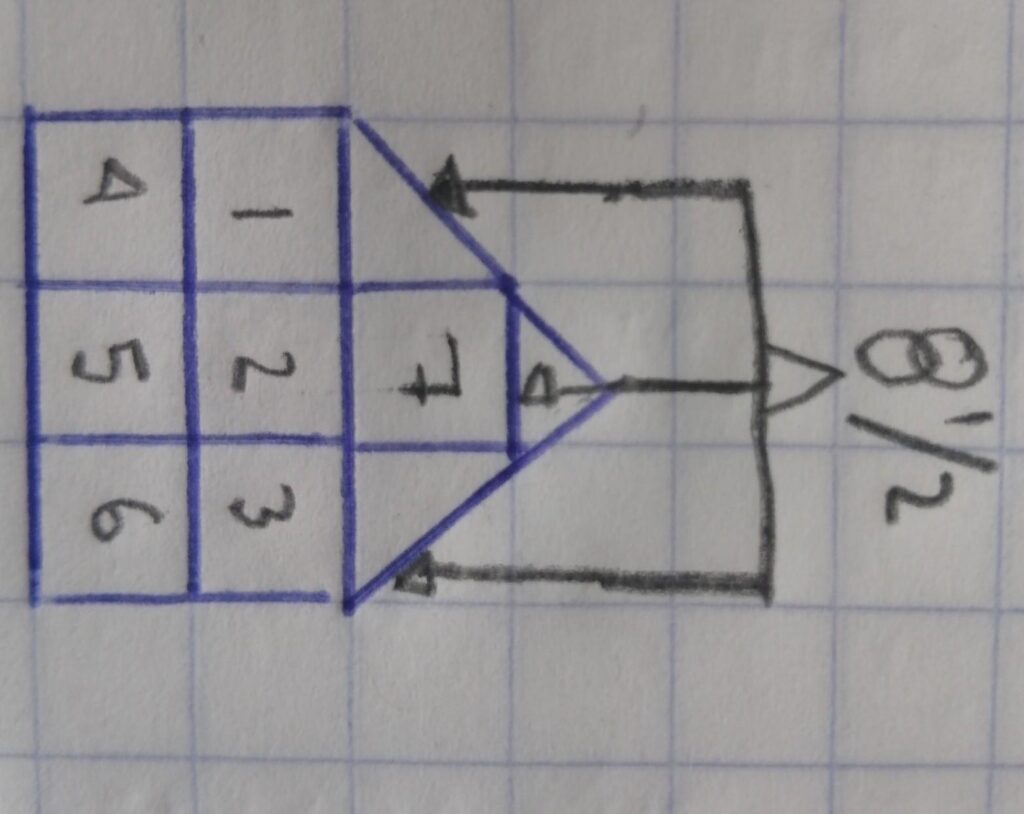
En el mundo de la geometría, la medida del área es fundamental para calcular cuánto espacio ocupa una figura en un plano. En este artículo, hablaremos de una figura que tiene una medida de área específica: 8 1/2 unidades cuadradas.
Para comenzar, es importante tener en cuenta que existen diferentes tipos de figuras geométricas que pueden tener esta medida de área. Por ejemplo, un rectángulo de 2 unidades de ancho y 4 1/4 unidades de largo tendría una medida de área de 8 1/2 unidades cuadradas. De igual forma, un cuadrado de 2 1/92 unidades de lado también tendría esta misma medida de área.
En general, cualquier figura que tenga una base y una altura que, multiplicadas, den como resultado 17/2, tendría una medida de área de 8 1/2 unidades cuadradas. Esto incluye triángulos, trapecios y otras formas irregulares.
Para entender mejor cómo se calcula el área de una figura, es importante conocer la fórmula básica. En el caso de un rectángulo, por ejemplo, el área se calcula multiplicando la base por la altura. Es decir: Área = base x altura. En el ejemplo anterior, la base del rectángulo es de 2 unidades y la altura es de 4 1/4 unidades. Al multiplicar ambos valores, obtenemos 8 1/2 unidades cuadradas.
Es importante mencionar que existen figuras más complejas, como círculos y elipses, cuyo cálculo de área es un poco más complicado. En estos casos, se necesitan utilizar fórmulas específicas para cada figura.
Para visualizar mejor cómo diferentes figuras pueden tener la misma medida de área, podemos compararlas en una tabla HTML. A continuación, se muestra una tabla con algunas de las figuras que tienen una medida de área de 8 1/2 unidades cuadradas:
| Figura | Base | Altura | Área |
|---|---|---|---|
| Rectángulo | 2 unidades | 4 1/4 unidades | 8 1/2 unidades cuadradas |
| Cuadrado | 2 1/92 unidades | 2 1/92 unidades | 8 1/2 unidades cuadradas |
| Triángulo | 6 unidades | 2 5/6 unidades | 8 1/2 unidades cuadradas |
| Trapecio | 3 unidades (base menor) | 5 2/3 unidades (base mayor) | 8 1/2 unidades cuadradas |
Además de las fórmulas y las tablas, también podemos utilizar analogías para entender mejor cómo funciona el cálculo de áreas. Podemos pensar en una figura como si fuera un pastel, donde la base sería la bandeja y la altura sería el grosor del pastel. Al cortar el pastel en diferentes formas, podemos obtener diferentes áreas, pero siempre manteniendo la misma cantidad de masa total.
En conclusión, La medida de área es fundamental para entender la geometría y el espacio que ocupan las figuras en un plano. Una figura que tenga 8 1/2 unidades cuadradas de área puede tomar diferentes formas, desde un rectángulo hasta un triángulo o un trapecio. Conociendo las fórmulas y utilizando analogías, podemos entender mejor cómo se calcula el área y cómo podemos aplicarlo en diferentes situaciones.
Preguntas frecuentes:
1. ¿Cómo se calcula el área de un círculo?
Para calcular el área de un círculo, se utiliza la fórmula A = πr², donde "r" es el radio del círculo y "π" es una constante aproximada a 3.14.
2. ¿Puede una figura tener una medida de área negativa?
No, la medida de área siempre es un valor positivo o cero. Una figura que tenga una medida de área negativa no tendría sentido en términos geométricos.
3. ¿Cómo se calcula el área de una elipse?
El cálculo del área de una elipse es un poco más complicado que otras figuras. La fórmula general es A = πab, donde "a" y "b" son los semiejes mayor y menor de la elipse, respectivamente.
4. ¿Por qué es importante conocer la medida de área de una figura?
Conocer la medida de área de una figura es esencial en muchas áreas de la vida, como la construcción, la ingeniería y la arquitectura. También es importante en matemáticas y ciencias en general, ya que nos ayuda a entender mejor el espacio y la geometría.
5. ¿Es posible que dos figuras tengan la misma medida de área pero formas diferentes?
Sí, es posible. Como hemos visto en este artículo, diferentes figuras pueden tener la misma medida de área. Esto se debe a que el cálculo del área depende de la base y la altura de la figura, y no necesariamente de su forma.

Deja una respuesta