Valor de z para un nivel de confianza de 95

Si estás familiarizado con la estadística, probablemente hayas oído hablar del valor de z. Es un término que se utiliza en la prueba de hipótesis y en la estimación de intervalos de confianza. El valor de z es una medida de la desviación estándar de una población en relación con su media. En otras palabras, el valor de z indica cuántas desviaciones estándar se encuentra un punto de datos por encima o por debajo de la media.

Uno de los usos más comunes del valor de z es en la construcción de intervalos de confianza. Los intervalos de confianza son un rango de valores que se utiliza para estimar el valor de una población. Los intervalos de confianza se calculan a partir de una muestra de datos y se expresan como un porcentaje de confianza. Por ejemplo, un intervalo de confianza del 95% significa que si se tomaran muchas muestras de la misma población, el 95% de esos intervalos contendrían el verdadero valor de la población.

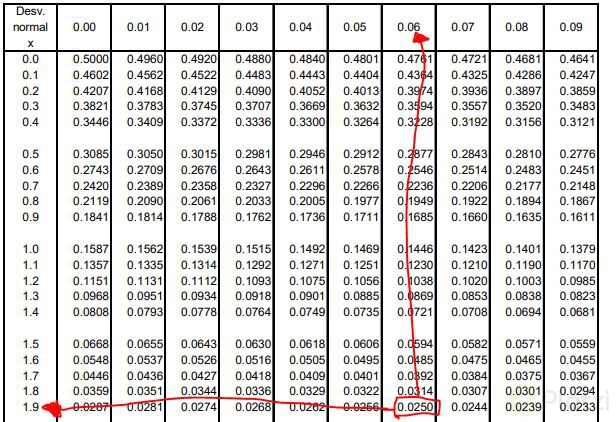
Para calcular el valor de z para un nivel de confianza del 95%, es necesario utilizar la distribución normal estándar. La distribución normal estándar es una curva que representa la distribución de probabilidad de una variable aleatoria que tiene una media de cero y una desviación estándar de uno. La distribución normal estándar se utiliza para estandarizar las puntuaciones de una variable aleatoria, de manera que se puedan comparar con otras distribuciones normales.

El valor de z para un nivel de confianza del 95% es de 1.96. Esto significa que si se construye un intervalo de confianza del 95% a partir de una muestra de datos, el margen de error será de más o menos 1.96 desviaciones estándar de la media. Por ejemplo, si se tiene una muestra de datos con una media de 50 y una desviación estándar de 10, el intervalo de confianza del 95% sería de 50 ± (1.96 x 10), o sea, de 30.4 a 69.6.

Es importante tener en cuenta que el valor de z para un nivel de confianza del 95% es solo uno de los muchos valores de z que se pueden utilizar en la estadística. El valor de z varía según el nivel de confianza deseado. Por ejemplo, el valor de z para un nivel de confianza del 99% es de 2.58, mientras que el valor de z para un nivel de confianza del 90% es de 1.645.

En resumen, El valor de z para un nivel de confianza del 95% es de 1.96. Este valor se utiliza en la construcción de intervalos de confianza para estimar el valor de una población a partir de una muestra de datos. El valor de z varía según el nivel de confianza deseado y es importante tener en cuenta que solo se aplica a distribuciones normales.

Tabla de valores de z

A continuación, se presenta una tabla de valores de z para diferentes niveles de confianza:

| Nivel de confianza | Valor de z |
|--------------------|------------|
| 80% | 1.28 |
| 85% | 1.44 |
| 90% | 1.645 |
| 95% | 1.96 |
| 99% | 2.58 |

¿Cómo se calcula el valor de z?

El valor de z se calcula utilizando la fórmula:

z = (x - μ) / σ

Donde:

- x es el valor de la variable aleatoria.
- μ es la media de la población.
- σ es la desviación estándar de la población.

Por ejemplo, si se tiene una población con una media de 50 y una desviación estándar de 10, y se quiere calcular el valor de z para un valor de x de 60, se utilizaría la fórmula:

z = (60 - 50) / 10 = 1

¿Por qué es importante el valor de z?

El valor de z es importante porque se utiliza en la prueba de hipótesis y en la construcción de intervalos de confianza. Estas son herramientas fundamentales en la estadística para tomar decisiones informadas basadas en los datos. El valor de z permite comparar los datos de una muestra con los de una población y determinar si hay una diferencia significativa entre ellos.

¿Qué es la distribución normal estándar?

La distribución normal estándar es una distribución de probabilidad que tiene una media de cero y una desviación estándar de uno. Esta distribución es importante en la estadística porque muchas variables aleatorias se pueden aproximar a una distribución normal. Al estandarizar las puntuaciones de una variable aleatoria utilizando la distribución normal estándar, se pueden comparar con otras distribuciones normales.

¿Qué es un intervalo de confianza?

Un intervalo de confianza es un rango de valores que se utiliza para estimar el valor de una población a partir de una muestra de datos. Los intervalos de confianza se expresan como un porcentaje de confianza y se calculan utilizando la distribución normal estándar y el valor de z correspondiente al nivel de confianza deseado. Por ejemplo, un intervalo de confianza del 95% significa que si se tomaran muchas muestras de la misma población, el 95% de esos intervalos contendrían el verdadero valor de la población.

¿Cómo se utiliza el valor de z en la prueba de hipótesis?

En la prueba de hipótesis, el valor de z se utiliza para determinar si hay una diferencia significativa entre los datos de una muestra y los de una población. Se compara el valor de z calculado a partir de la muestra con el valor de z correspondiente al nivel de significancia deseado. Si el valor de z calculado es mayor que el valor de z correspondiente al nivel de significancia, se rechaza la hipótesis nula y se acepta la hipótesis alternativa.