X 2 y 2 1 3 x 2y 3 0

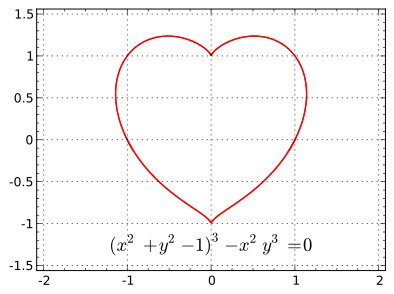
El término "X 2 y 2 1 3 x 2y 3 0" puede parecer confuso y abrumador para aquellos que no están familiarizados con la notación matemática. Sin embargo, en realidad es una simple ecuación polinómica que puede ser resuelta utilizando métodos de álgebra básica.

Para entender mejor esta ecuación, primero debemos descomponerla en términos más simples. Primero, notamos que hay dos variables presentes: x e y. Luego, podemos separar los términos en dos partes: los que contienen x y los que contienen y. Así, la ecuación se puede escribir como:

x^2 + y^2 - 3x + 2y^3 = 0

Ahora, podemos ver que esta es una ecuación de segundo grado en x y una ecuación de tercer grado en y. Podemos resolver esta ecuación de varias maneras, pero una forma común es utilizar el método de sustitución.

Comencemos por despejar x en términos de y. Para hacer esto, podemos reorganizar la ecuación para obtener:

x^2 - 3x = -y^2 + 2y^3

Luego, podemos utilizar la fórmula cuadrática para encontrar las soluciones para x en términos de y:

x = (3 ± √(9 + 4y^2 - 8y^3)) / 2

Ahora, podemos utilizar estas soluciones para x y sustituirlas en la ecuación original para encontrar las soluciones para y. Después de algunos cálculos, podemos encontrar que hay tres soluciones para esta ecuación:

y = 0, y = 1/2, y = 1

Para cada valor de y, podemos encontrar los valores correspondientes de x utilizando las soluciones que encontramos anteriormente.

En resumen, La ecuación "X 2 y 2 1 3 x 2y 3 0" es simplemente una ecuación polinómica que puede ser resuelta utilizando métodos de álgebra básica. Si bien puede parecer confusa al principio, con un poco de descomposición y sustitución, podemos encontrar fácilmente sus soluciones.