La derivada de una funcion en un punto x representa

La derivada de una función en un punto x es un concepto fundamental en el cálculo diferencial. Si bien puede parecer una idea abstracta y difícil de comprender, en realidad es una herramienta muy útil para entender cómo cambia una función en un punto específico.

En términos simples, la derivada de una función en un punto x representa la tasa de cambio instantánea de la función en ese punto. Es decir, indica cuánto cambia la función en un instante muy pequeño alrededor del punto x.

Para entender mejor este concepto, imaginemos que estamos conduciendo un automóvil y queremos saber a qué velocidad estamos viajando en un momento específico. Si tomamos la velocidad promedio de los últimos 5 minutos, podemos tener una idea aproximada de nuestra velocidad actual, pero no será una medida exacta. En cambio, si miramos el velocímetro en un momento específico, podemos ver nuestra velocidad exacta en ese momento.

De manera similar, la derivada de una función en un punto x nos da una medida exacta de cómo cambia la función en ese punto. Esto es especialmente útil cuando queremos conocer la velocidad o la aceleración de una función en un punto específico.

Para calcular la derivada de una función en un punto x, utilizamos la fórmula de la derivada, que es la siguiente:

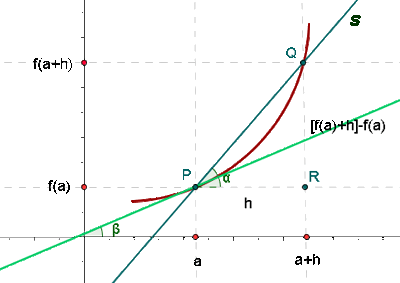
f'(x) = lim(h->0) (f(x+h) - f(x))/h

Esta fórmula puede parecer complicada a primera vista, pero en realidad es bastante sencilla de entender. Lo que hace es calcular la tasa de cambio de la función entre los puntos x y x+h, y luego tomar el límite cuando h se acerca a cero para obtener la tasa de cambio instantánea en el punto x.

Una vez que tenemos la derivada de una función en un punto x, podemos utilizarla para muchas cosas diferentes. Por ejemplo, podemos determinar si una función es creciente o decreciente en ese punto, si tiene un máximo o un mínimo local, si es cóncava o convexa, y mucho más.

En resumen, La derivada de una función en un punto x representa la tasa de cambio instantánea de la función en ese punto. Es una herramienta fundamental en el cálculo diferencial y nos permite entender mejor cómo cambian las funciones en puntos específicos.

Tabla de comparación

Para ilustrar mejor la idea de la derivada en un punto, podemos compararla con una tabla HTML. En una tabla HTML, cada celda representa un valor específico de una variable. En la misma línea, podemos pensar en una función como una tabla, donde cada punto en el eje x corresponde a un valor de la variable y cada punto en el eje y corresponde a un valor de la función.

La derivada en un punto x es como una celda en la tabla HTML: nos da información específica sobre la función en ese punto. Al igual que una celda puede contener diferentes tipos de datos, como texto, números o imágenes, la derivada de una función también puede tomar diferentes formas, dependiendo de la función.

Usando listas para ejemplificar

Otra forma de entender la derivada en un punto x es compararla con una lista HTML. En una lista HTML, cada elemento de la lista tiene un índice específico. Si queremos acceder a un elemento específico, podemos simplemente buscar su índice y encontrar el valor correspondiente.

De manera similar, podemos pensar en una función como una lista, donde cada punto en el eje x corresponde a un índice y cada punto en el eje y corresponde a un valor de la función. La derivada en un punto x es como el valor de un elemento específico en la lista: nos da información sobre la función en ese punto específico.

Conclusión

La derivada de una función en un punto x es una herramienta fundamental en el cálculo diferencial. Nos permite entender cómo cambia una función en un punto específico y nos da información valiosa sobre la función en general. Si bien puede parecer un concepto abstracto al principio, con un poco de práctica y comprensión, podemos utilizar la derivada para resolver una amplia gama de problemas matemáticos.

Preguntas frecuentes

¿Qué es una derivada?

Una derivada es una medida de la tasa de cambio instantánea de una función. Nos da información sobre cómo cambia la función en un punto específico.

¿Por qué es importante la derivada?

La derivada es importante porque nos permite entender cómo cambian las funciones en puntos específicos. Es una herramienta fundamental en el cálculo diferencial y se utiliza en muchas áreas de las matemáticas y la ciencia.

¿Cómo se calcula la derivada?

La derivada se calcula utilizando la fórmula de la derivada, que es lim(h->0) (f(x+h) - f(x))/h. Esta fórmula nos permite calcular la tasa de cambio instantánea de la función en un punto específico.

¿Qué es una función cóncava?

Una función cóncava es una función cuya gráfica se curva hacia abajo en lugar de hacia arriba. Se dice que una función es cóncava si su segunda derivada es negativa.

¿Qué es una función creciente?

Una función creciente es una función cuya gráfica se mueve hacia arriba a medida que avanzamos hacia la derecha. Es decir, la función aumenta a medida que el valor de la variable independiente aumenta.