Relacion entre teoria de conjuntos logica matematica y algebra booleana
La teoría de conjuntos, la lógica matemática y el álgebra booleana son tres ramas de las matemáticas que están estrechamente relacionadas entre sí. De hecho, la teoría de conjuntos es la base de la lógica matemática y el álgebra booleana es una aplicación directa de la lógica matemática. En este artículo, exploraremos la relación entre estas tres ramas de las matemáticas y cómo se complementan entre sí.
Teoría de conjuntos
La teoría de conjuntos es una rama de las matemáticas que estudia los conjuntos, que son colecciones de objetos. La teoría de conjuntos se desarrolló en el siglo XIX gracias a los trabajos de Georg Cantor, quien fue el primero en utilizar la teoría de conjuntos para investigar los números reales. La teoría de conjuntos se utiliza en muchas áreas de las matemáticas, incluyendo la geometría, la topología, el análisis matemático y la teoría de la computación.
La teoría de conjuntos utiliza símbolos matemáticos para representar los conjuntos y las operaciones que se pueden realizar con ellos. Los símbolos más comunes son:
- A ⊂ B: "A es un subconjunto de B"
- A ∪ B: "la unión de A y B"
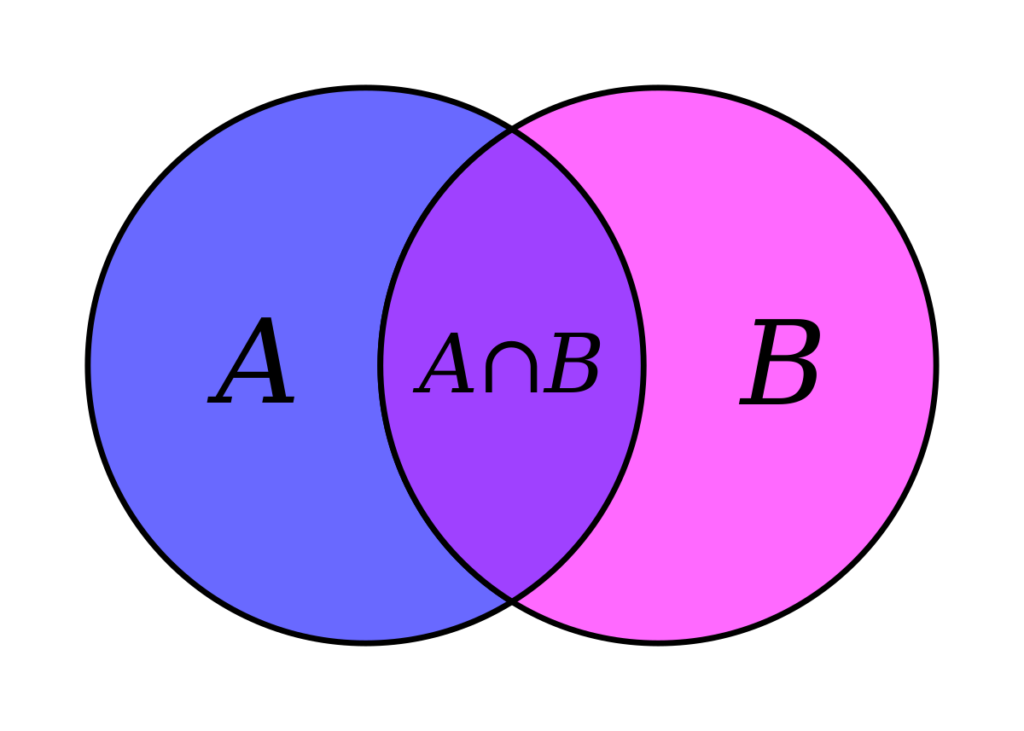
- A ∩ B: "la intersección de A y B"
- A' o ¬ A: "el complemento de A"
Lógica matemática
La lógica matemática es una rama de las matemáticas que se ocupa de las leyes del razonamiento y la inferencia. La lógica matemática se utiliza en muchas áreas de las matemáticas, incluyendo la teoría de la computación, la teoría de la información y la inteligencia artificial.
La lógica matemática utiliza símbolos para representar proposiciones y conectores lógicos para combinar proposiciones. Los símbolos más comunes son:
- p: "proposición p"
- q: "proposición q"
- ¬ p: "no p"
- p ∧ q: "p y q"
- p ∨ q: "p o q"
- p → q: "si p entonces q"
- p ↔ q: "p si y solo si q"
Álgebra booleana
El álgebra booleana es una rama del álgebra que se ocupa de las operaciones lógicas binarias y su aplicación a los circuitos electrónicos y la programación de computadoras. El álgebra booleana se basa en las leyes de la lógica matemática y utiliza los símbolos 0 y 1 para representar los valores lógicos verdadero y falso.
El álgebra booleana utiliza operadores lógicos para combinar valores lógicos. Los operadores más comunes son:
- ¬: "no"
- ∧: "y"
- ∨: "o"
- →: "si entonces"
- ↔: "si y solo si"
Relación entre teoría de conjuntos, lógica matemática y álgebra booleana
La relación entre la teoría de conjuntos, la lógica matemática y el álgebra booleana es estrecha y se basa en la utilización de símbolos y operadores. La teoría de conjuntos es la base de la lógica matemática, ya que los conjuntos se pueden utilizar para representar proposiciones y los operadores de conjuntos se pueden utilizar para combinar proposiciones.
La lógica matemática es la base del álgebra booleana, ya que los operadores lógicos se pueden utilizar para combinar valores lógicos y los símbolos 0 y 1 se pueden utilizar para representar los valores lógicos verdadero y falso.
El álgebra booleana se utiliza en la programación de computadoras y en el diseño de circuitos electrónicos, ya que los circuitos electrónicos se pueden describir mediante ecuaciones booleanas y los programas de computadora se pueden escribir utilizando lógica booleana.
Tabla de comparación
A continuación, se muestra una tabla que compara los conceptos más importantes de la teoría de conjuntos, la lógica matemática y el álgebra booleana:
| Concepto | Teoría de conjuntos | Lógica matemática | Álgebra booleana |
|------------------|-------------------------|---------------------------|-----------------------|
| Representación | Conjuntos | Proposiciones | Valores lógicos |
| Operadores | ∪, ∩, ' | ¬, ∧, ∨, →, ↔ | ¬, ∧, ∨, →, ↔ |
| Uso | Geometría, análisis | Teoría de la computación | Programación, circuitos |
| Base | Números | Razonamiento | Operaciones lógicas |
| Símbolos | ⊂, ⊆, ∪, ∩ | p, q, ¬, ∧, ∨, →, ↔ | 0, 1, ¬, ∧, ∨, →, ↔ |
Preguntas frecuentes
¿Por qué la teoría de conjuntos es importante?
La teoría de conjuntos es importante porque proporciona una base sólida para otras áreas de las matemáticas, como la geometría, la topología y el análisis matemático. La teoría de conjuntos también se utiliza en la teoría de la computación y en la inteligencia artificial.
¿Qué es la lógica matemática?
La lógica matemática es una rama de las matemáticas que se ocupa de las leyes del razonamiento y la inferencia. La lógica matemática utiliza símbolos para representar proposiciones y conectores lógicos para combinar proposiciones.
¿Qué es el álgebra booleana?
El álgebra booleana es una rama del álgebra que se ocupa de las operaciones lógicas binarias y su aplicación a los circuitos electrónicos y la programación de computadoras. El álgebra booleana se basa en las leyes de la lógica matemática y utiliza los símbolos 0 y 1 para representar los valores lógicos verdadero y falso.
¿Cómo se utiliza el álgebra booleana en la programación de computadoras?
El álgebra booleana se utiliza en la programación de computadoras para la toma de decisiones lógicas. Los programas de computadora se pueden escribir utilizando lógica booleana, utilizando operadores lógicos como ∧, ∨, ¬, → y ↔ para combinar expresiones booleanas.
¿Cómo se utiliza el álgebra booleana en el diseño de circuitos electrónicos?
El álgebra booleana se utiliza en el diseño de circuitos electrónicos para describir el comportamiento de los circuitos en términos de ecuaciones booleanas. Los circuitos electrónicos se pueden describir utilizando operaciones booleanas como ∧, ∨, ¬, → y ↔.

Deja una respuesta